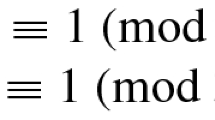Abstract
We describe the use of the Boyer-Moore theorem prover in mechanically generating a proof of the Law of Quadratic Reciprocity: for distinct odd primes p and q, the congruences x 2 ≡q (mod p) and x 2 ≡p (mod q) are either both solvable or both unsolvable, unless p≡q≡3 (mod 4). The proof is a formalization of an argument due to Eisenstein, based on a lemma of Gauss. The input to the theorem prover consists of nine function definitions, thirty conjectures, and various hints for proving them. The proofs are derived from a library of lemmas that includes Fermat's Theorem and the Gauss Lemma.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Guass, K. F., Disquisitiones Arithmeticae, translated by A. Clarke, Yale U. Press (1966).
Dunnington, G., Carl Friedrich Gauss: Titan of Science, Exposition Press, New York (1955).
Artin, E. and Tate, J., Class Field Theory, Benjamin, New York (1968).
Boyer, R. S. and Moore, J S., A Computational Logic, Academic Press, New York (1979).
Boyer, R. S. and Moore, J S., A Computational Logic Handbook, Academic Press, Boston (1988).
Nagell, T., Introduction to Number Theory, Chelsea Press, New York (1964).
Boyer, R. S. and Moore, J S., ‘Proof checking the RSA public key encryption algorithm’, Am. Math. Monthly 91, 181–189 (1984).
Russinoff, D. M., ‘An experiment with the Boyer-Moore theorem prover: a proof of Wilson's theorem’, J. Automated Reasoning 1, 121–139 (1985).
Russinoff, D. M., ‘A mechanical proof of quadratic reciprocity’, Tech. Report STP-389-90, MCC, Austin, TX (1990).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Russinoff, D.M. A mechanical proof of Quadratic Reciprocity. J Autom Reasoning 8, 3–21 (1992). https://doi.org/10.1007/BF00263446
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF00263446