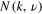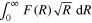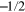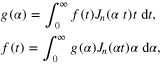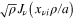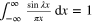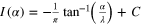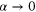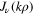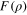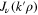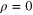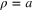Abstract
The rigorous proof of the orthogonality integral 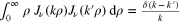 , for
, for 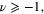 is laborious and requires the use of mathematical techniques that, probably, are unfamiliar to most physics students, even at the graduate level. In physics, we are used to the argument that it may be proved by the use of Hankel transforms. However, the logic of the matter is the opposite, i.e., the existence of the inverse Hankel transform is a consequence of the orthogonality integral. The goal of this work is to prove this integral without circular reasoning. In this paper, using elementary properties of Bessel functions, we give a simple analytical derivation of this integral for the case where ν is an integer, zero, or half-integer not less than
is laborious and requires the use of mathematical techniques that, probably, are unfamiliar to most physics students, even at the graduate level. In physics, we are used to the argument that it may be proved by the use of Hankel transforms. However, the logic of the matter is the opposite, i.e., the existence of the inverse Hankel transform is a consequence of the orthogonality integral. The goal of this work is to prove this integral without circular reasoning. In this paper, using elementary properties of Bessel functions, we give a simple analytical derivation of this integral for the case where ν is an integer, zero, or half-integer not less than 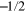 . Then, using the asymptotic behaviour of
. Then, using the asymptotic behaviour of 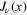 , we extend the result to any
, we extend the result to any 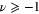 . This work is of a pedagogical nature. Therefore, to add educational value to the discussion, we do not skip the details of the calculations.
. This work is of a pedagogical nature. Therefore, to add educational value to the discussion, we do not skip the details of the calculations.
1. Introduction
The Bessel differential equation appears in a wide variety of physical problems, including static potentials in electromagnetism, propagation of waves in cylindrical waveguides, solutions of the radial Schrödinger equation, modes of oscillation of thin plates and membranes, and heat conduction [1].
In cylindrical coordinates 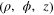 the assumption that the solution of the Laplace equation can be found as the superposition of functions of the form
the assumption that the solution of the Laplace equation can be found as the superposition of functions of the form 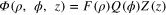 leads to three ordinary differential equations, one for each function. The equation for the radial function
leads to three ordinary differential equations, one for each function. The equation for the radial function  is given by
is given by
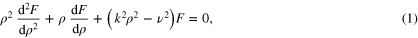
where k and ν are separation constants, k has dimensions of (length) and ν is dimensionless. If the physical problem shows translational symmetry along the z-axis, then k = 0. Similarly, if it shows rotational symmetry about z, then
and ν is dimensionless. If the physical problem shows translational symmetry along the z-axis, then k = 0. Similarly, if it shows rotational symmetry about z, then  .
.
When k is real and positive, it is customary to introduce the dimensionless variable

in terms of which (1) becomes

This is the well-known Bessel differential equation of order  , whose general solution is customarily written as
, whose general solution is customarily written as

where  and
and  are linearly independent solutions of (3) called Bessel functions of the first kind and Bessel functions of the second kind, respectively. These functions have been thoroughly studied in the literature [2–4] and, thus, one could hardly add something substantial to what is already known about them.
are linearly independent solutions of (3) called Bessel functions of the first kind and Bessel functions of the second kind, respectively. These functions have been thoroughly studied in the literature [2–4] and, thus, one could hardly add something substantial to what is already known about them.
Therefore, our interest in this note is of a pedagogical nature. Here, we consider the problem of finding a simple analytical derivation of the integral relation
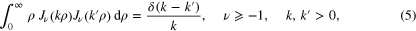
which is the statement that Bessel functions 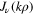 , with different values of k, are orthogonal on the infinite range
, with different values of k, are orthogonal on the infinite range 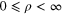 with respect to the weight
with respect to the weight 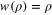 . The proof of the orthogonality of these functions on a finite interval,
. The proof of the orthogonality of these functions on a finite interval, 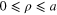 , is a standard procedure that is widely discussed in many books and textbooks. However, this is not so when the interval is infinite.
, is a standard procedure that is widely discussed in many books and textbooks. However, this is not so when the interval is infinite.
The above integral follows from Hankelʼs integral theorem1
. In section 14.4 of [4], Watson provides an elaborate and thorough proof of Hankelʼs integral theorem for 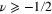 . The proof is quite long, almost eight pages in length, and is more difficult when the range of ν is extended to
. The proof is quite long, almost eight pages in length, and is more difficult when the range of ν is extended to  . The complexity of the proof is probably the reason why the discussion of the orthogonality of the Bessel functions
. The complexity of the proof is probably the reason why the discussion of the orthogonality of the Bessel functions 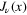 over an infinite interval is avoided.
over an infinite interval is avoided.
In physics, generally we are not very much concerned with the details of the proofs of mathematical theorems. Usually, we are more interested in their application for analysing and solving physical problems. This happens, in particular, with the orthogonality relation (5). In the monograph Mathematical Methods for Physicists [5], the integral (5) with 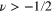 is given, without proof, in section 11.2 (equation (11.59)). Later, in the same reference (problem
is given, without proof, in section 11.2 (equation (11.59)). Later, in the same reference (problem 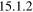 ), the inverse Hankel transform is assumed in such a way that it allows one to obtain (5) in a line of calculation2
. However, the truth of the matter is in the opposite direction: the inversion formula is a consequence of (5). Clearly, this is circular logic where the conclusion is part of the premises3
.
), the inverse Hankel transform is assumed in such a way that it allows one to obtain (5) in a line of calculation2
. However, the truth of the matter is in the opposite direction: the inversion formula is a consequence of (5). Clearly, this is circular logic where the conclusion is part of the premises3
.
For several purposes it is useful when physics students, especially those of theoretical physics, have a clear notion of the mathematical foundations underlying the theory; it improves students' confidence and enhances their critical thinking. In Jacksonʼs Classical Electrodynamics [6], in problem 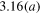 , the verification of (5) is left as an exercise to the reader, with the hint of using Besselʼs differential equation and the appropriate limiting procedures. It should be noted that despite the large number of solutions books and websites (for example [7–11]) for many of the problems in Jackson, most of them either do not address the problem or do it in an incorrect way.
, the verification of (5) is left as an exercise to the reader, with the hint of using Besselʼs differential equation and the appropriate limiting procedures. It should be noted that despite the large number of solutions books and websites (for example [7–11]) for many of the problems in Jackson, most of them either do not address the problem or do it in an incorrect way.
The paper is organized as follows. In section 2, we give a simple analytical derivation of the orthogonality integral (5) for the case where ν is an integer, zero, or half-integer not less than 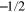 . In section 3, using the asymptotic behaviour of
. In section 3, using the asymptotic behaviour of  , we obtain by means of direct calculation the orthogonality integral (5) for an arbitrary
, we obtain by means of direct calculation the orthogonality integral (5) for an arbitrary 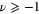 . In section 4, we give a summary and discussion.
. In section 4, we give a summary and discussion.
2. Fourier–Bessel expansion
To make the presentation self-consistent, we start from the Fourier–Bessel series over a finite interval  and then consider the case where the interval becomes infinite
and then consider the case where the interval becomes infinite  . We will show that the orthogonality integral (5) is a consequence of the fact that
. We will show that the orthogonality integral (5) is a consequence of the fact that 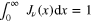 .
.
Since 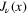 oscillates about 0, the equation
oscillates about 0, the equation  has an infinite number of roots:
has an infinite number of roots: 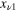 ,
, 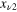 ,
,  .... When a is finite, these roots play an important role. First, the functions
.... When a is finite, these roots play an important role. First, the functions 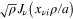 , with fixed
, with fixed  and different i, are mutually orthogonal in the interval
and different i, are mutually orthogonal in the interval 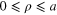 , i.e.
, i.e.
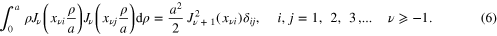
Second, any piecewise smooth function  on the interval
on the interval 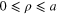 can be expanded in a Fourier–Bessel series4
can be expanded in a Fourier–Bessel series4
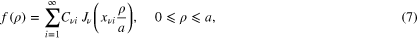
where the coefficients  are obtained with the help of the orthogonality condition (6) as
are obtained with the help of the orthogonality condition (6) as
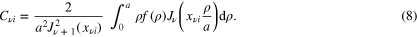
When 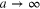 , the discrete superposition in (7) is replaced by a continuous superposition. In this limit, the chain of formal transformations
, the discrete superposition in (7) is replaced by a continuous superposition. In this limit, the chain of formal transformations
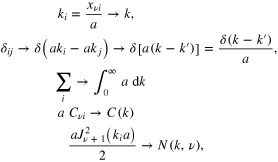
where the 'normalization factor'  is still unknown, changes the set of equations (6)–(8) into
is still unknown, changes the set of equations (6)–(8) into
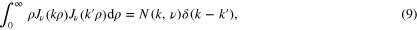

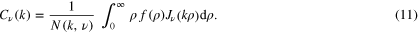
Since the norm of 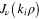 on a finite interval depends on ν, we assume that N is also a function of ν. To check the compatibility of these equations, we multiply both sides of (10) by
on a finite interval depends on ν, we assume that N is also a function of ν. To check the compatibility of these equations, we multiply both sides of (10) by 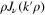 and integrate over ρ from zero to infinity. Then, using (11), we obtain
and integrate over ρ from zero to infinity. Then, using (11), we obtain
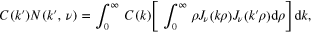
which is an identity by virtue of (9).
Finally, the closure relation
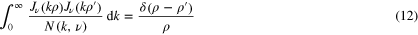
is obtained when we substitute (11) into (10).
To find the unknown normalization factor  , we integrate both sides of (9) over
, we integrate both sides of (9) over  from zero to infinity and obtain
from zero to infinity and obtain
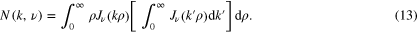
To give an analytical derivation of (5), as promised in the introduction, we need to calculate these integrals manually, without the aid of computers or tables of integrals. Below, we do this for the case where ν is an integer, zero, or half-integer.
2.1. Evaluating the Integrals
From the recurrence relation
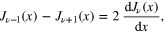
it follows that
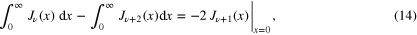
where we have used that  , for an arbitrary ν. Since
, for an arbitrary ν. Since
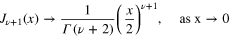
the rhs of (14) is zero for 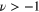 . Consequently
. Consequently
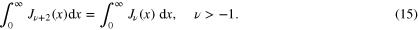
Odd integer order: when 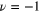 , the rhs of (14) is equal to −2, because
, the rhs of (14) is equal to −2, because 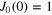 . Thus, using that
. Thus, using that 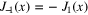 , we obtain
, we obtain

From this expression and (15), we get
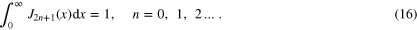
Even integer order: when ν is an even number, to obtain a similar relation, we need to calculate  . Since
. Since
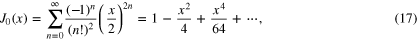
we cannot integrate term by term. Instead, we use the Parseval integral

which is easy to verify; expanding in series around x = 0 and integrating over θ, we obtain (17).
Thus
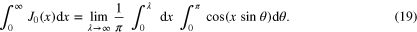
• Straightforward evaluation of  : assuming that we can change the order of integration, we obtain
: assuming that we can change the order of integration, we obtain
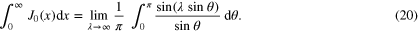
The function under the integral, in the rhs of (20), possesses mirror symmetry with respect to 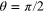 . It tends to λ when
. It tends to λ when 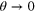 , as well as when
, as well as when  , and in between it becomes zero
, and in between it becomes zero  times, where
times, where  represents the largest integer not greater than
represents the largest integer not greater than
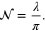
Therefore, in the limit 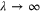 this function vanishes everywhere except for the two infinitely high and infinitely narrow peaks at
this function vanishes everywhere except for the two infinitely high and infinitely narrow peaks at  and
and 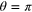 . This suggests that, in this limit the integrand in the rhs of (20) can be expressed as a combination of Dirac delta functions.
. This suggests that, in this limit the integrand in the rhs of (20) can be expressed as a combination of Dirac delta functions.
A useful representation of the delta function comes from the theory of the Fourier integral. Namely5
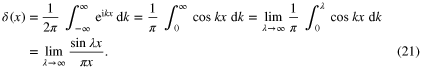
From this expression, it follows that the rhs of (20) is  . At this point, we recall that when the Dirac delta function has as argument a function f(s), with simple zeros located at
. At this point, we recall that when the Dirac delta function has as argument a function f(s), with simple zeros located at  , it reduces to
, it reduces to

Consequently
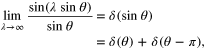
in agreement with the above discussion. Thus, we obtain
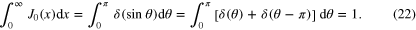
• Alternative evaluation of  : for pedagogical reasons, it is worth mentioning that (19) can be evaluated, without the explicit use of Diracʼs delta function, by solving the integral
: for pedagogical reasons, it is worth mentioning that (19) can be evaluated, without the explicit use of Diracʼs delta function, by solving the integral

which in the limit  yields
yields 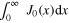 .
.
The integral over x in (23) is easily done after using Eulerʼs formula 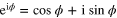 to express the cosine in terms of exponents. The result is
to express the cosine in terms of exponents. The result is
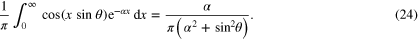
Thus
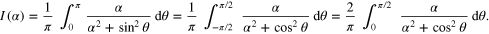
To evaluate the last integral, we use the variable 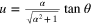 , in terms of which
, in terms of which
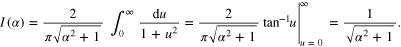
In the limit  , we get
, we get 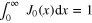 , in agreement with (22).
, in agreement with (22).
It may seem somewhat surprising that we obtain the expected result without using the Dirac delta function. However, the delta function appears in the limit of 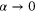 since
since
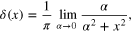
and the rhs of (24) becomes  . Thus, in this limit (23) reduces to (22).
. Thus, in this limit (23) reduces to (22).
In conclusion, we have shown that  . Then, from (15), we get
. Then, from (15), we get
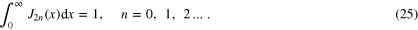
Half-integer order: Bessel functions of half-integer order are elementary functions. For 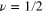 , we have
, we have
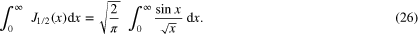
To evaluate this integral, we first introduce the variable
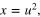
in terms of which (26) becomes
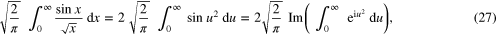
where we have used Eulerʼs formula and 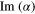 means the complex part of the complex number α.
means the complex part of the complex number α.
Next, we make a second change of variables, i.e. 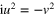 so that
so that 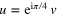 . In terms of this new variable, (27) becomes
. In terms of this new variable, (27) becomes
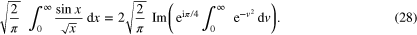
Since
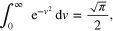
we obtain
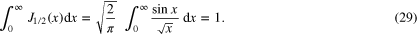
In a similar way, we get
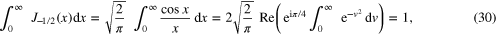
where Re 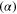 means the real part of the complex number α.
means the real part of the complex number α.
Consequently, using (15), we get
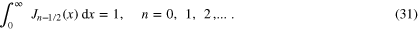
• Collecting the results given by (16), (25), and (31), we have shown that

for any integer, zero, or half-integer  .
.
To extend this result to an arbitrary ν, we would have to use an integral representation for 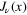 valid for all values of ν. However, this is beyond the scope of the present note.
valid for all values of ν. However, this is beyond the scope of the present note.
2.2. Finding the factor 
As mentioned earlier (2), in physical problems  . Therefore, when x varies from 0 to infinity, either k or ρ should be kept fixed. If k remains fixed and
. Therefore, when x varies from 0 to infinity, either k or ρ should be kept fixed. If k remains fixed and 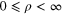 , then (32) yields
, then (32) yields

Similarly, if ρ remains fixed and 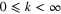 , then
, then

With these two integrals at hand, the task of finding of 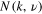 is straightforward. Namely, from (13) we get
is straightforward. Namely, from (13) we get

Thus, N is independent of ν.
As a consequence of (35), the orthogonality integral (9) and the closure integral (12) become completely symmetric under the change 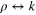 , i.e.
, i.e.
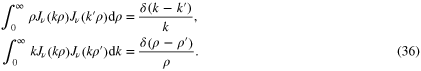
Similarly, the Fourier–Bessel transform is also symmetric if we change 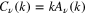 , namely,
, namely,


In this notation, 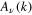 is the νth-order Hankel transform of
is the νth-order Hankel transform of 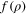 . Reciprocally,
. Reciprocally, 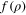 is the νth-order Hankel transform of
is the νth-order Hankel transform of  ; in short, it is called the inverse Hankel transform.
; in short, it is called the inverse Hankel transform.
To finish this section, we would like to remark that we are perfectly aware that the integrals considered here are tabulated and can be found, for example, in [12]. If we use that table of integrals, or some computational software program, we can readily verify the validity of (5), for any ν. However, although fast and simple, such a verification would have no, or little, educational value because it teaches nothing about the Bessel functions nor develops technical or analytical skills6 .
3. Generalization to an arbitrary 
In this section, we use the asymptotic behaviour of Bessel functions 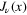 to demonstrate that
to demonstrate that  , for all
, for all 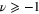 . In addition, we explain why this factor is independent of ν.
. In addition, we explain why this factor is independent of ν.
To this end, we consider the limit
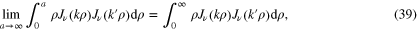
where the integral in the lhs is given by7
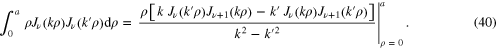
• To evaluate this expression at  , we use the asymptotic expression of
, we use the asymptotic expression of  for small values of ρ,
for small values of ρ,
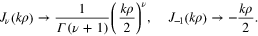
Substituting into (40), we get
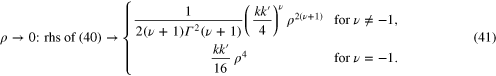
Consequently, for any  the lower limit of (40) is zero.
the lower limit of (40) is zero.
• To compute the limit  , we first evaluate (40) for
, we first evaluate (40) for 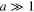 . To this end, we use the large ρ behaviour of
. To this end, we use the large ρ behaviour of 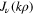 , i.e.
, i.e.
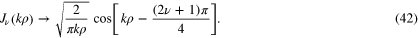
Substituting this into the rhs of (40), we find
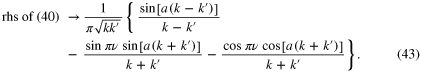
We note that the denominator in the last two expressions never vanishes, because k and 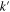 are positive.
are positive.
Next, in the limit  we have
we have


The first expression follows from (21). To verify (45) we take the limit in two steps. First, we introduce the small parameter ξ as follows:
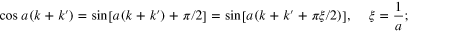
then, we expand in series around  and rearrange terms to obtain
and rearrange terms to obtain
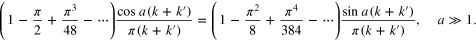
Finally, in the limit  the rhs yields
the rhs yields  , which justifies (45).
, which justifies (45).
Thus, in the limit  the second and third terms in (43) are proportional to
the second and third terms in (43) are proportional to 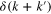 , which is nonzero only when
, which is nonzero only when 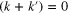 . Given that k and
. Given that k and  are positive, in this limit their contribution to (39) is zero. The only term that survives is the first one, which is proportional to
are positive, in this limit their contribution to (39) is zero. The only term that survives is the first one, which is proportional to  . Consequently, from (9) and (39) we get
. Consequently, from (9) and (39) we get

3.1. Role of phase shift
To elucidate why N(k) is independent of ν, we write (42) as
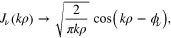
where the explicit form of the phase  is irrelevant. Using this, we obtain
is irrelevant. Using this, we obtain
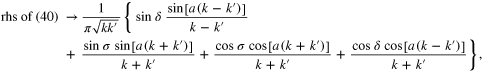
where
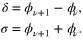
In the limit 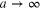 , the second and third terms are proportional to
, the second and third terms are proportional to 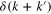 , and therefore they do not contribute to (39) regardless of σ. Meanwhile, the first and fourth terms are proportional to
, and therefore they do not contribute to (39) regardless of σ. Meanwhile, the first and fourth terms are proportional to 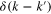 . The fourth term vanishes when
. The fourth term vanishes when 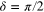 . Consequently, the normalizing factor (46) turns out to be independent of ν because, for large arguments,
. Consequently, the normalizing factor (46) turns out to be independent of ν because, for large arguments,  and
and  are shifted by a phase
are shifted by a phase 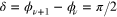 , i.e.
, i.e. 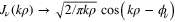 and
and 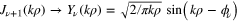 .
.
4. Summary and discussion
The rigorous proof of the orthogonality integral (5) is laborious and requires the use of mathematical techniques that, probably, are unfamiliar to most physics students, even at the graduate level.
In physics, to make calculations more feasible, we often reduce the problems by making simplifying hypotheses, which have reasonable physical meaning but are not always well supported mathematically. This is epitomized by problem 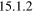 of [5]. In that problem, the orthogonality integral (5) is obtained, in one line of calculation, from the Hankel transform and its inverse (see footnote 2).
of [5]. In that problem, the orthogonality integral (5) is obtained, in one line of calculation, from the Hankel transform and its inverse (see footnote 2).
However, this is an exercise of circular reasoning (see footnote 3) that does not prove the orthogonality integral. In practice, the technique of orthogonal functions and expansions works in the opposite way: first we identify an appropriate set of orthonormal functions and then use it as a basis to expand other functions.
It should be noted that the orthogonality relationship (5) discussed here is between Bessel functions of the same order ν, which have the same functional form but have distinct constants in the arguments. This is different from other common orthogonal functions used in physics (e.g., Legendre/Hermite/Laguerre polynomials), where the orthogonality is between functions of different order—i.e., corresponding to different eigenvalues—which have different functional forms but the same argument.
In section 2, we used elementary properties of Bessel functions 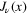 to compute
to compute  . For ν integer, zero, or half-integer
. For ν integer, zero, or half-integer 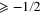 , we obtained
, we obtained  . From this, we found the normalization factor
. From this, we found the normalization factor  . As a consequence, the orthogonality integral and the closure integral (36) become symmetrical under the change
. As a consequence, the orthogonality integral and the closure integral (36) become symmetrical under the change  . Also, the integrals (10) and (11) turn into Hankel transforms. The merit of this approach is its simplicity. The shortcoming is that our calculation is limited to the case where ν is an integer, zero, or a half-integer no less than
. Also, the integrals (10) and (11) turn into Hankel transforms. The merit of this approach is its simplicity. The shortcoming is that our calculation is limited to the case where ν is an integer, zero, or a half-integer no less than  .
.
In section 3, using the asymptotic behaviour of 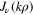 , we obtained the factor N(k) by means of direct calculation. The advantage of this approach, which is probably the one suggested by Jackson in his problem 3.16, is that it works for any
, we obtained the factor N(k) by means of direct calculation. The advantage of this approach, which is probably the one suggested by Jackson in his problem 3.16, is that it works for any 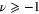 . Additionally it allows us to understand why this factor is independent of ν. The disadvantage, however, could be the level of mathematical rigor used to evaluate the limit
. Additionally it allows us to understand why this factor is independent of ν. The disadvantage, however, could be the level of mathematical rigor used to evaluate the limit 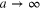 in (43). Apart of this, one is left with the false sense that one has succeeded in proving Hankelʼs integral theorem, when the truth is that many of the details of the demonstration are skipped when using the asymptotic form (42).
in (43). Apart of this, one is left with the false sense that one has succeeded in proving Hankelʼs integral theorem, when the truth is that many of the details of the demonstration are skipped when using the asymptotic form (42).
Although the techniques used in sections 2 and 3 appear to be mutually different, they are complementary; the bridge between them is attained at a higher mathematical level when using contour integral representations of  , which is beyond the scope of this work. From a pedagogical point of view, they serve not only as a source of validation of Hankelʼs integral theorem but also as a way to develop valuable technical and analytical skills that can be applied to broader issues.
, which is beyond the scope of this work. From a pedagogical point of view, they serve not only as a source of validation of Hankelʼs integral theorem but also as a way to develop valuable technical and analytical skills that can be applied to broader issues.
Footnotes
- 1
The statement of Hankelʼs integral theorem, in Watsonʼs notation ([4], section 14.4) is: let F(R) be an arbitrary function of the real variable R subject to the condition that
 exists and is absolutely convergent; and let the order ν of Bessel functions be not less than
exists and is absolutely convergent; and let the order ν of Bessel functions be not less than  . Then
. Then
provided that the positive number r lies inside an interval in which F(R) has limited total fluctuation.
- 2
For the sake of clarity and self-consistency, the problem
 of [5] is: assuming the validity of Hankel transform-inverse transformation transform pair of equations
of [5] is: assuming the validity of Hankel transform-inverse transformation transform pair of equations
show that the Dirac delta function has a Bessel integral representation

- 3
Circular reasoning: logical fallacy in which the reasoner begins with what they are trying to end with (http://en.wikipedia.org/wiki/Circular_reasoning).
- 4
The word 'any' assumes that the set of functions
 , with ν fixed and
, with ν fixed and  , is complete.
, is complete. - 5
The straightforward demonstration of
 requires techniques of contour integration in the complex plane [13]. However, this can be demonstrated 'the Feynman way' using nothing but elementary calculus by evaluating the integral
requires techniques of contour integration in the complex plane [13]. However, this can be demonstrated 'the Feynman way' using nothing but elementary calculus by evaluating the integral  , with
, with  and the condition that
and the condition that  (http://ocw.mit.edu/courses/mathematics/18-304-undergraduate-seminar-in-discrete-mathematics-spring-2006/projects/integratnfeynman.pdf). Assuming that we can differentiate under the integral we get
(http://ocw.mit.edu/courses/mathematics/18-304-undergraduate-seminar-in-discrete-mathematics-spring-2006/projects/integratnfeynman.pdf). Assuming that we can differentiate under the integral we get 
Consequently,
 , where C is a constant of integration. Since
, where C is a constant of integration. Since  we find
we find  . Thus
. Thus  . In the limit
. In the limit  we get
we get 
- 6
This is authorʼs opinion, as theoretical physicist. However, in modern times, the concept of what has or does not have educational value can be controversial. It all depends on the objectives of education, which in turn rely upon market requirements.
- 7
The recipe for this equation is as follows: (i) multiply (1), with
 replacing
replacing  , by
, by  ; (ii) in the equation thus obtained change
; (ii) in the equation thus obtained change  ; (iii) subtract the latter from the former to obtain
; (iii) subtract the latter from the former to obtain
(iv) use the recurrence relation
 ; (v) integrate from
; (v) integrate from  to
to  .
.