1. Introduction
Geng & Huang (2015) proposed that Fast Radio Bursts (FRBs) may be powered by collisions between Neutron Stars (NSs) and asteroids/comets, and Dai et al. (2016) studied the radiation mechanisms of such collisions while proposing that repeating FRBs could be explained by NSs traveling through asteroid belts.
Rotating Radio Transients (RRATs) have durations and frequencies similar to FRBs, but they originate in the Milky Way galaxy and their luminosities are a billion times fainter (McLaughlin et al. 2006).
'Oumuamua and CNEOS 2014-01-08 represent the first interstellar asteroids (ISAs) larger than dust discovered in the Solar System (Meech et al. 2017; Siraj & Loeb 2019a), serving as calibrations for the ISA size distribution (Siraj & Loeb 2019b).
In this Note, we explore the possibility that ISAs could power a subclass of RRATs which do not repeat over long timescales.
2. Emission Mechanism
Assuming the radiation mechanism in Dai et al. (2016) for an NS with radius ∼12.5 km (Abbott et al. 2018), the luminosity per unit frequency at 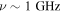 is,
is,

where MNS is the NS mass, μNS is the NS magnetic dipole moment, κ is a constant describing the asteroid composition, s is the tensile strength of the asteroid, ρ is the mass density of the asteroid, and r is the radius of the asteroid. Dai et al. (2016) also show the duration of the emission to be of order a millisecond.
3. Method
We adopt the three-dimensional velocity dispersions for stars in the thin disk of the Milky Way as a proxy for the kinematics of ISAs (Bland-Hawthorn & Gerhard 2016). We take the velocity distribution of NS (relative to the LSR) to be a two-component Gaussian described by the following probability function (Faucher-Giguere & Kaspi 2005):

where w1 = 0.90, σ1 = 160 km s−1, and σ2 = 780 km s−1.
We use a Monte Carlo method to determine the characteristic relative speed of NS–ISA collisions, and find the median relative speed to be,  .
.
Assuming that the distributions of ISAs and NSs follow the distribution of stars (Faucher-Giguere & Kaspi 2005), we define  and ζNS ≡ nNS/n⋆.
and ζNS ≡ nNS/n⋆.
The cumulative Earth impact rate for an ISA of radius r is estimated to be  (Siraj & Loeb 2019b). Assuming that ∼5% of all asteroids are composed primarily of iron1
, and given the Earth's apparent cross section as well as the characteristic ISA velocity dispersion of ∼20 km s−1, we find the number density of ISAs of radius ≥r to be related to the number density of stars by a factor of,
(Siraj & Loeb 2019b). Assuming that ∼5% of all asteroids are composed primarily of iron1
, and given the Earth's apparent cross section as well as the characteristic ISA velocity dispersion of ∼20 km s−1, we find the number density of ISAs of radius ≥r to be related to the number density of stars by a factor of,

where  is the number density of stars in the solar neighborhood.
is the number density of stars in the solar neighborhood.
The minimum luminosity at a frequency of ν ∼ 1 GHz for a source at a distance d to be visible with a detector of flux threshold f is,

yielding the minimum ISA radius that produces a visible flare,

thereby allowing us to express ζISA in terms of d and f as,

We model the Milky Way galaxy as a disk with a radial scale length Rd ∼ 3 kpc and vertical scale height h ∼ 0.1R as a function of radial distance R and vertical distance z,

Given ζNS = 1.7 × 10−3, we compute randomly generated positions of 108 NSs (Sartore et al. 2010) in the Galaxy (following the density of stars), and subsequently find the distance between each one and the Earth. We then find the rate at which each NS produces flares at or above the limiting flux f as measured from Earth to be,

where vrel is drawn from the aforementioned Monte Carlo method. Finally, we sum individual rates. The minimum asteroid radius considered, rmin, is given approximately by the minimum size at which an asteroid is tidally disrupted before it reaches its melting point. Cordes & Shannon (2008) and Geng & Huang (2015) conclude that rmin ∼ 1 m, as below this size, an iron asteroid will melt before it is tidally disrupted.
4. Rate
We find the all-sky rate of observable NS–ISA flares to be described as the following fitting function,

Figure 1 shows the rate as a function of rmin along with an associated fitting function.
Figure 1. Rate of ∼1 Jy radio flares at ν ∼ 1 GHz from NS–ISA collisions.
Download figure:
Standard image High-resolution image5. Conclusions
We have shown that NS–ISA collisions could reliably power observable, non-repeating, millisecond-duration ∼1 GHz radio flares in the Milky Way galaxy. We would not expect to detect any X-ray emission from such events, given the expression for X-ray flux in Dai et al. (2016) for rmin ≳ 1 m. We do not expect such events to constitute a significant fraction of FRBs, both within and outside of the Milky Way galaxy.
The abundance of single-pulse RRATs is still poorly constrained (Agarwal, McLaughlin & Lorimer, private communication).
This work was supported in part by a grant from the Breakthrough Prize Foundation.
Footnotes
- 1
The reason we consider objects primarily composed of iron is because Dai et al. (2016) focus on impacts for iron-rich asteroids.




