Introduction

There is a strong demand in the field of applied sciences such as architecture, agriculture, and medicine, etc., for climatological and biometeorological methods and means of calculation that are easily understandable. The radiation and human-bioclimate model RayMan (Matzarakis et al. 2007) meets this demand. Despite its simplicity, RayMan provides good simulation results for radiation flux densities and thermo-physiologically significant assessment indices. Use of RayMan-derived results in applied sciences has many advantages (Mayer 1993; VDI 1998; Thorsson et al. 2004; Johansson and Emmanuel 2006; Matzarakis et al. 2007).

The human energy balance can be applied to the evaluation of the impact of the thermal component of climate on humans. This method has been used in several studies (e.g. Jendritzky et al. 1990; Höppe 1993; VDI 1998; Mayer et al. 2008). Under clear sky conditions in summer, short-wave radiation flux densities exhibit the greatest variation amongst all meteorological parameters, particularly in urban areas. The human-biometeorological influence of short- and long-wave radiation flux densities can be transferred into a synthetic parameter, the mean radiant temperature T mrt (Jendritzky et al. 1990; Höppe 1993; Mayer 1993; VDI 1998). T mrt is defined as the uniform temperature of a hypothetical spherical surface surrounding a human (emissivity ε = 1) that would result in the same net radiation energy exchange with the subject as the actual, complex radiative environment. The latter usually varies considerably under open space conditions.

Existing methods for the calculation of short- and long-wave radiation flux densities are applied mostly to the analysis of radiation conditions at horizontal surfaces. For human-biometeorological studies, the radiation environment of the human body has to be considered in a three-dimensional way. Several models and software packages designed to calculate radiation and thermal comfort conditions in several ways and with various input possibilities now exist (ENVI-met, Bruse and Fleer 1998; Radtherm, www.thermoanalytics.com; Townscope, Teller and Azar 2001). In addition, methods for the calculation of short-wave radiation flux densities also exist. These techniques apply both simple and complex models with different time resolutions on the basis of different existing calculation methods (Valko 1966; Brühl and Zdunkowski 1983; Jessel 1983; Olseth and Skartveit 1993; VDI 1994; Badescu 1997; Ceballos and de Moura 1997; Meek 1997; Gul et al. 1998; Mora-Lopez and Sidrach-de-Cardona 1998; Kemmoku et al. 1999; Marki and Antonic 1999; Roderick 1999; Santamouris et al. 1999; Craggs et al. 2000; Gueymard 2000). Models using sunshine duration for the calculation of short-wave radiation flux densities are used (Valko 1966; Gopinathan 1992; Revfeim 1997; Sen 1998) as well as simple parameterisations for turbidity (Kasten 1980; Power 2001). Methods for the calculation of long-wave radiation flux densities are also available (Czeplak and Kasten 1987; Salsibury and D’Aria 1992; Diak et al. 2000; Nunez et al. 2000; Prata 1996; Iziomon and Mayer 2001; Iziomon et al. 2003). For complex situations in urban settings, several models and analytic methods are documented in the literature (Kaempfert 1949, 1951; Terjung and Louie 1974; Mohsen 1979; Frank et al. 1981; Zdunkowski and Brühl 1983; Littlefair 2001; Kanda et al. 2005).

The main purpose of this paper is to present a method for the simulation of T mrt for thermal human-biometeorological studies on different space and time scales by use of the RayMan model. Additionally, sunshine duration and shadow in simple and complex environments are included in the model. The model is compatible with Windows® and can analyse complex urban structures and other environments. The model requires only basic meteorological data (air temperature, air humidity and wind speed) for the simulation of radiation flux densities and common thermal indices for the thermal human-bioclimate. In this paper, a comparison between results from possibilities of model runs and measurements is discussed.

Scientific background and methods

Mean radiant temperature

Cause and effect relations between the atmospheric environment and human health or human comfort can be analysed by a human-biometeorological classification (Kerslake 1972; ISO 1983; Jendritzky et al. 1990; VDI 1998; Matzarakis et al. 2007). The thermal component of the climate is an important factor and can be described and quantified in a thermo-physiologically significant way by thermal indices.

In summer, the mean radiant temperature T mrt is the most significant meteorological input parameter for the human energy balance because of its modification by clouds as well as topographical and urban morphologies (Winslow et al. 1936; Clark and Edholm 1985). Therefore, T mrt has the strongest influence on thermo-physiological significant indices like physiologically equivalent temperature (PET) or standard effective temperature (SET*; Mayer 1993; Gagge et al. 1986; Höppe 1999) in many climate environments. Here, the modelling/calculation of T mrt only is presented.

For long-term studies without direct measurement of radiation flux densities, T mrt can be simulated using models. In the literature, methods to estimate radiation flux densities based on parameters including air temperature, air humidity, degree of cloud cover, atmospheric turbidity, time of day, and day of the year are recommended (Jendritzky et al. 1990; Matzarakis et al. 2007). However, both the albedo of the surrounding surfaces and their solid angle proportions must be specified in these models. Additionally, other factors such as the geometrical properties of buildings, vegetation, reflexion properties, etc., have to be taken into account. For the application of such models in simple situations, the following radiation flux densities are required:

  • direct solar radiation,

  • diffuse solar radiation,

  • reflected short-wave radiation,

  • atmospheric radiation (long-wave) from the open sky,

  • long-wave radiation from solid surfaces (lower hemisphere and horizon limitation).

The following parameters describing the surroundings of the human body must be known:

  • sky view factor—because of the limitation of the horizon and the influence of short- and long-wave radiation flux densities,

  • view factor of the different solid surfaces—because of the modification of the reflected short-wave radiation,

  • albedo of the different solid surfaces—because of the influence of the incoming short-wave radiation,

  • emissivity of the different solid surfaces—because of the influence on the surface temperature.

To calculate T mrt, the entire surroundings of the human body are divided into n isothermal surfaces with the temperatures T i (i = 1 to n) and emissivities εi, for which the solid angle portions (“angle factors”) F i are used as weighting factors. Long-wave radiation (E i = εi*σ*T 4i ) and diffuse short-wave radiation, Di, are emitted from each of the n surfaces of the surroundings (Fanger 1972; Jendritzky et al. 1990). This results in an approach for T mrt (Fanger 1972; Jendritzky and Nübler 1981) as:

$$ {T_{mrt}} = {\left[ {\frac{1}{\sigma }\sum\limits_{i = 1}^n {\left( {{E_i} + {a_k}\frac{{{D_i}}}{{{\varepsilon _p}}}} \right){F_i}} } \right]^{0.25}} $$
(1)

where σ is the Stefan-Boltzmann constant [5.67*10−8 W/(m2K4)] and εp is the emission coefficient of the human body (standard value 0.97). D i comprises the diffuse solar radiation and the diffusely reflected global radiation, whereas ak is the absorption coefficient of the irradiated body surface area of short-wave radiation (standard value 0.7).

Tmrt is incremented to T*mrt, if there is also direct solar radiation (Jendritzky et al. 1990):

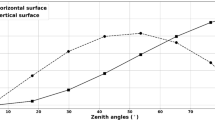
$$ T{*_{mrt}} = {\left[ {{T_{mrt}}^4 + \frac{{{f_p}{a_k}{I^*}}}{{\left( {{\varepsilon _p}\sigma } \right)}}} \right]^{0.25}} $$
(2)

In this case, I* is the radiation intensity of the sun on a surface perpendicular to the incident radiation direction. The surface projection factor \( {f_p} = 0.30{\text{8 cos}}\left( {\gamma ~\left( {0.998 - {\gamma^2}} \right)/50000} \right) \) for the sun elevation angle γ (in degrees) is a function of the incident radiation direction and the body posture (VDI 1998, 2001; Jendritzky et al. 1990). For applications in human-biometeorology, it is generally sufficient to determine fp for a rotationally symmetrical person standing or walking (Jendritzky et al. 1990).

Estimation of radiation fluxes and T mrt by the RayMan model

The RayMan model is Windows-based software with the code written in Delphi. The model offers several estimation and input possibilities (described above and in Matzarakis et al. 2007). Here, only the method of estimation of the radiation flux densities and T mrt is described. The model divides the three-dimensional environment into an upper and a lower hemisphere. Usually, the lower hemisphere has a sky view factor f svf that is covered by solid surfaces. So, for the lower hemisphere the adjustment of the solid properties is easier than for the upper hemisphere. For the lower hemisphere, the albedo and emissivity have to been known in order to simulate the short- and long-wave radiation flux densities from the lower hemisphere (reflected short- and long-wave emission from the ground, see Fig. 1). The parting plane between the two hemispheres is at 1.1 m a.g.l., which represents the weighting centre of the human body (Fanger 1972; Jendritzky et al. 1990).

Fig. 1
figure 1

Radiation flux densities important for the determination of the mean radiant temperature (T mrt)

Full size image

The distribution of the solid and free sky elements and their amount in the upper hemisphere are required for the estimation of the radiation flux density of the upper hemisphere. These elements can be attributed to a pixel map, e.g. of a fish-eye photograph (Fig. 2) or a rendered image of a vector model. Each pixel, p i, in Fig. 2 corresponds to an angle factor F i located at the azimuth angle α i and the zenith angle ζ i. The angle factor is weighted by \( {F_i} = 1/\left( {\pi {N^2}/4} \right){ \sin }\left( {{\zeta_i}} \right)/{\zeta_i} \), where ζ i is determined via \( {\zeta_i} = {\left( {\Delta x_i^2 + \Delta y_i^2} \right)^{1/2}}\pi /N \) by the pixel distance Δx i and Δy i of p i from the centre of the N × N pixels sized image in the x and y direction, respectively. Pixels with ζ i > π/2 (i.e. below the horizon) are ignored. Summing up all F i values results in the sky view factor f svf. T mrt is obtained via Eqs. 1 and 2 together with the short- and long-wave radiation flux densities.

Fig. 2
figure 2

Fish-eye photographs under the canopy of a group of trees (upper) and for a semi-open place (lower) in Freiburg. The circle in the upper image marks an opening in the tree crown

Full size image

Estimation of global radiation

The global radiation G o for undisturbed conditions (free horizon and no clouds) can be estimated as follows (Jendritzky et al. 1990; VDI 1994, 1998):

$$ {G_0} = 0.84 \cdot {I_0} \cdot \cos \zeta \cdot \exp \left( { - 0.027 \cdot \frac{\rho }{{{\rho_0}}} \cdot {T_L}/\cos \zeta } \right) $$
(3)

with the solar radiation flux density I 0 (W/m²), the zenith angle ζ (°) of the sun, the local atmospheric pressure p (hPa) relative to the normal pressure p 0 = 1,013 hPa at sea level, and the Linke turbidity factor T L. However, for real-life applications this assumption is barely adequate. A better approach for G is the sum of the direct and the diffuse solar radiation, I and D, respectively, which both take horizon limitations and cloudiness into account.

For the direct radiation I on a horizontally oriented surface, the formulation is (Jendritzky et al. 1990):

$$ I = {I_0} \cdot \cos \zeta \cdot \exp \left( { - {T_L} \cdot {\delta_{r0}} \cdot {m_{r0}} \cdot \frac{\rho }{{{\rho_0}}}} \right){\kern 1pt} \; \cdot \left( {1 - \frac{N}{8}} \right) $$
(4)

if the sun is not masked by an obstacle. I o is the irradiance of extraterrestrial solar radiation on the plane normal to the direction of incidence for the current solar distance (W/m2). N denotes the degree of cloudiness in octas, δ op the vertical optical thickness of the standard (Rayleigh) atmosphere, and m r0 the relative optical air mass, which considers the extended optical path through the atmosphere for zenith angles ζ > 0 with respect to vertical incidence. Kasten and Young (1989) provided an equation for the relative optical air mass

$$ {m_{R0}} = 1/\left( {\sin \gamma + 0.50572 \cdot {{\left( {\gamma + 6.07995^\circ } \right)}^{ - 1.6364}}} \right) $$
(5)

with the solar altitude angle \( \gamma = 90^\circ - \zeta \). The optical thickness can be calculated (Kasten 1980) by

$$ {\delta_{R0}} = 1/\left( {0.9{m_{r0}} + 9.4} \right) $$
(6)

for zenith angles ζ < 85° (i.e. γ > 5°). For higher values of ζ (gazing incidence), an approximation according to Table 1 with linear interpolation for intermediate values satisfies. If the ___location of interest is in the shade, then I = 0.

Table 1 Vertical optical thickness δr0 for gazing incidence; intermediate values are interpolated linearly
Full size table

According to Valko (1966), the diffuse radiation can be composed linearly of the two extreme values for cloudless (N = 0) and overcast (N = 8) conditions:

$$ D = {D_0} \cdot \left( {1 - \frac{N}{8}} \right) + {D_8} \cdot \frac{N}{8} $$
(7)

D 0, in turn, comprises an isotropic (D iso) and an anisotropic (D aniso) component, \( {D_0} = {D_{\text{iso}}} + {D_{\text{aniso}}} \). It holds that

$$ {D_{iso}} = \left( {{G_0} - I\left( {N = 0} \right)} \right) \cdot \left( {1 - \tau } \right) \cdot {f_{svf}} $$
(8)

where \( \tau = I\left( {N = 0} \right)/\left( {{I_0}\;{ \cos }\;\zeta } \right) \) is the transmittance of the direct solar radiation represented by the exponential term in Eq. 4. f svf allows for horizontal limitations due to the topography, surrounding buildings, etc. Since the anisotropic radiation tends to concentrate in the vicinity of the sun, the calculation is discriminated depending on whether the sun is directly visible. Thus, no f svf is taken into account in

$$ {D_{aniso}} = \left( {{G_0} - I\left( {N = 0} \right)} \right) \cdot \tau $$
(9)

for the case where the sun is not hidden by the horizontal limitation, otherwise D aniso = 0. Finally, the (fully isotropic) overcast component is approximately

$$ {D_8} = {G_0} \cdot \left( {1 - 0.72} \right) \cdot {f_{svf}} = 0.28\,{G_0} \cdot {f_{svf}} $$
(10)

Estimation of atmospheric radiation

For the (long wave) atmospheric radiation, we used the Angstrom formula because it uses only general atmospheric parameters (air temperature and vapour pressure) and the mean cloud cover in octas without distinguishing between different cloud types and layers (Falkenberg and Bolz 1949; Monteith 1990; Oke 1987; VDI 1994):

$$ A = \sigma \cdot T_a^4 \cdot \left( {0.82 - 0.25 \cdot {{10}^{ - 0.0945 \cdot {V_p}}}} \right) \cdot \left( {1 + 0.21 \cdot {{\left( {\frac{N}{8}} \right)}^{2.5}}} \right) $$
(11)

Here, the air temperature T a in K, the vapour pressure V p in hPa and the degree of cloudiness N in octas are the required variables.

Estimation of the long-wave radiation flux density emitted by solid surfaces

Furthermore, the long-wave radiation E being emitted from solid surfaces can be expressed by

$$ E = \varepsilon \cdot \sigma \cdot T_s^4 + \left( {1 - \varepsilon } \right) \cdot A $$
(12)

The first part of the sum represents the thermal emission from a surface with temperature T s (K). The second part is the non-absorbed (thus reflected) fraction of the incident long-wave radiation, which is dominated by the atmospheric radiation A in first approximation. The surface temperature can be initially estimated using air temperature and subsequently calculated (Oke 1987) via:

$$ {T_s} = {T_a} + \frac{Q + B}{{\left( {6.2 + 4.26 \cdot {v_{wind}}} \right) \cdot \left( {1 + \frac{1}{B_O}} \right)}} $$
(13)

with the net all-wave radiation flux density Q, the soil flux B = −0.19 Q if Q > 0 and −0.32 Q if Q < 0, the wind velocity v wind and the Bowen ratio B o. Since \( Q = {a_k}G + A-E \) incorporates E, both values E and T s can be calculated iteratively with Eqs. 12 and 13. All energy flux densities are given in W m−2.

Results

Validation of the model

RayMan has been tested in different environments, especially for studies with urban morphologies. It can be used for a range of purposes. In the following section, two tests of the RayMan model on different data sets are outlined.

The surroundings can be modelled basically in two ways: (1) by importing fish-eye photographs, and (2) by detailed description of obstacles such as buildings and trees by their geometrical properties (see Matzarakis et al. 2007). The vector model utilizes much more detailed information of the surroundings, which all has to be determined and declared.

In the following comparison, we used the fish-eye model since it is much easier to insert despite being the more complex means of estimating T mrt.

Comparison of global radiation

Figure 3 presents the measured and simulated global radiation for four days in July 2006 (16–19) in Freiburg. The measured data are taken from the urban meteorological station Freiburg (Matzarakis and Mayer 2008) located on the roof of a tall building at 52 m a.g.l. in the northern part of the city of Freiburg. The simulated values for global radiation shown in Fig. 3 fit the measured values very well. Usually, the differences between modelled and measured global radiation range from −20 to +20 W/m2 during sunshine hours and can be explained as an effect of turbidity. Thus, for the estimation of T mrt, it is important to know the turbidity conditions. The differences increase to more than 20 W/m2 (modelled) in the afternoon when clouds affect the measured global radiation. The one small negative peak in the morning hours (about 10:30 CET) is a result of the effect of the rope of the mast of the station.

Fig. 3
figure 3

Measured and simulated global radiation for 16–19 July 2006 in Freiburg, Germany

Full size image

Measured and modelled mean radiant temperature in urban areas

The accuracy of simulations of the mean radiant temperature T mrt was tested over a period of 3 days in July 2006. The experimentally based determination of T mrt used a combination of a pyranometer and a pyrgeometer according to Höppe (1993) and Matzarakis et al. (2007). Here, measured and simulated T mrt are compared in two different environments. The fish-eye photos of the two points are shown in Fig. 2. The first point is under the canopy of a group of trees. Direct solar radiation, which can affect T mrt, passes the tree canopy only between 11.00 and 12.00 CET (marked by the circle in Fig. 2). The second point is about 30 m away from the first point and is a semi-open ___location surrounded by buildings and trees. This measurement ___location is not affected by any obstacles between 8.00 and 17.00 CET. Thus, the comparison is better for time periods with direct solar radiation. When the sun is very close to the edges of obstacles (buildings), small error or variations by the fish-eye pictures and exact time influence the results exorbitantly. This leads to a pronounced scattering of data points at the times mentioned. Figure 4 shows the daily courses of the measured and simulated T mrt under the tree canopy; both patterns are similar. The mean difference between measured and simulated T mrt is less than 2°C. For the semi-open ___location (Fig. 5), the mean T mrt difference shows a similar behaviour, with lower differences during times of high sun angle (between 10.00 and 15.00 CET from −6.4 to 6.1) with the highest measured value of 69.2°C. The highest differences occur at low sun angles in the morning and afternoon (−8.3 to 7.9°C). In general, the coefficient of determination, r, between measured and simulated T mrt (Fig. 6) for the semi-open place is 0.95 [root mean square error (RMSE) = 3.7 K] and for under the tree r is 0.96 (RMSE = 0.7 K).

Fig. 4
figure 4

Comparison between measured and simulated T mrt for the period 17–19 July 2006 in Freiburg under the canopy of a group of trees [Δ (M−S) is difference between measurement and simulation]

Full size image
Fig. 5
figure 5

Comparison between measured and simulated T mrt for the period 17–19 July 2006 in Freiburg in a semi-open place [Δ (M−S) is difference between measurement and simulation]

Full size image
Fig. 6
figure 6

Correlation between measured and simulated T mrt values for the sites described in Fig. 4

Full size image

Discussion and conclusion

Comparison of T mrt between measurements carried out at two locations in Freiburg (under trees and in semi-open space) shows that the differences under the tree canopy are low on average (less than 2°C). Only at low sun angles are the differences a little higher, particularly in the afternoon. This indicates that reflected radiation from vertical surfaces is not considered by the use of fish-eye photos. These effects become even more evident in the semi-open ___location, where differences during high sun angles are lower than in the late morning hours, during which the differences are higher (measured values are higher). This is because of the effect of the buildings and trees in the northern part of the space, which reflect radiation components. The additional reflection of these buildings (based on fish-eye photos) cannot be considered in the RayMan model, but these effects can be considered by the importance of their geometrical properties. On the one hand, short-wave radiation flux densities in complex environments are highly influenced by the reflection of obstacles. These effects can be seen in the morning hours and sometimes during midday in the semi-open space. Thorsson et al. (2007) found similar effects in their comparison. On the other hand, the simulated data for global radiation and also for the T mrt closely resemble the measured data (for both simple and complex environments with regards to global radiation properties).

Based on the comparison results it can be concluded that the RayMan model (based on fish-eye photos and geometrical properties of the surroundings) is a suitable tool for the simulation of radiation flux densities and T mrt, which are required for thermal comfort studies and related studies. Another advantage of the model is the short running time in comparison with other models. Note also that, in semi-open locations, the differences between measured and simulated T mrt are lower if the surroundings are based on truly geometrical properties.

The development of the RayMan model is not yet complete. It is planned to continue the development of RayMan, especially with regard to the import of computer-aided design (CAD) files and digital atlas data, which will allow a more straightforward calculation of the geometrical properties of urban structures and obstacles.

In general, there is a strong demand for human-biometeorological and urban climate models, not only in this research area itself, but also from urban planners and architects. The end users of the model obviously prefer easily understandable models that require only limited input data. RayMan is available for general use under (http://www.urbanclimate.net/rayman) and has an easy user-friendly interface.