Math Hombre

I must have three unfinished blogposts to get through, but this is what I keep coming back to this week.

Natasha Lewis Harrington is a doctoral psychology student who writes about my favorite game (Magic: the Gathering) in her spare time. Sometimes she crosses the stream to great effect. Like this week, when she wrote about why this game is so good at encouraging creativity among players. It's applying the work of (let me copy and paste here) Mihaly Csikzentmihalyi (specifically Creativity: Flow and the Psychology of Discovery and Invention [Google book preview]) to the question of how can we learn to engage more. I think it's well readable by non-Magic players, so please do peruse.

Here's the quick take:
(The little bit of art is from Flickr, Paolo Colacino who does what he calls generative art. Quite neat.)

Csikzentmihalyi has a TED talk about leaving boredom:


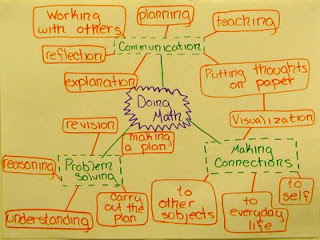
Why is this gripping me so? Because of the divide between math as taught and math as it could be.

Math, as it is often taught, violates all three of these principles. (1) We tell you the problems to do, (3) we insist on solo mastery and uniformity of method.

Wait, that's only two.

I'm wondering if I have, in my need to change (1) and (3), more than occasionally neglected (2). Is that the procedural knowledge which I de-emphasize?  I usually do that in an attempt to get the pendulum swinging in the other direction, but in doing so am I denying needed support?

Maybe not. Maybe Learning the System in mathematics is not the procedural stuff. Maybe it's the processes, hidden behind the procedural emphasis. (The processes now appearing with their new band, the Standards for Mathematical Practice.)

Of course, there's hope. Teachers like Fawn Nguyen, Michael Pershan and Andrew Stadel are knocking this engagement issue out of the park on all three principles.

But, as Dave Coffey has cautioned, and convinced me, we need to teach our students to take control of their own engagement. So when they leave Jim Pai's classroom, they can be engaged the next year, too.

That's empowerment, and that's what I want for my students.

I've been loving the posts people are writing for this year's virtual conference responding to the prompt: What is at the center of your classroom?. The conference is an amazing collection of writing put together by Riley Lark, blooger at Point of Inflection.  (Which I've always liked because it sounds - and reads - like he's synthesizing intention and reflection.)

This is an attempt to emulate my betters, which is actually not a bad strategy for improvement.

I want the center of my classroom to be empowerment. As a bad beginning teacher, emulating David Letterman of all people, I realized that I loved teaching math. I'd tell people that there weren't many things you could teach where the student would literally be able to do something at the end of the class that they couldn't do at the beginning.  While I still like that, I now think it can happen in  many more places than math class, and have a much different idea of what I want the students to be able to do.

On my own I got to realizing that problem solving was what I really wanted to teach, and my friend Sue Feeley introduced me to Polya (figuratively) and the other NCTM process standards.  Both helped give me language to describe things I had realized, and both indicated a path to set out on. Vygotsky helped me understand why students responded so differently to the same task.

Mosaic of Thought, Cambourne's Conditions of Learning and other literacy education work helped me start to understand how to teach processes, and I don't know that I would ever have found that were it not for Kathy and Dave Coffey. The conditions are the heart of what I want for my students, and creating or nurturing those conditions is what I see as the main responsibility of my work.

Engagement is first and foremost. Cambourne notes that engagement requires learners to believe:

• they are potential doers of what is being taught. This fits with and explains the idea that the students need to be the ones working in the classroom. (See also expectations)
• what they are doing matters to them. This is why teaching the processes is so important to me. Polynomial division does not matter to 99% of students. Problem solving will make 100% of my students' lives better.
• they are safe to try. This is why classroom community is so important. (See also approximation.)

Cambourne links engagement with two conditions:

• Immersion. Learners need to experience real and rich mathematics of all kinds.  Still one of my measures of how rich a question is is to consider how many processes it invites learners to engage in.
• Demonstration. Learners need many and authentic demonstrations of what they are learning. This was huge for me. I had become a hardcore discovery-based teacher. I was proud of my students saying things like "Why ask him, you know he won't tell us." (Oh, that is painful to me now.) I took students' feedback about their frustration and decided that it was because they weren't used to this mode of learning.  But really, I was asking them to do things they'd never seen.  Asking them to learn how to dance when they'd never seen one. Coupled with a lack of good feedback, it's a real testament to those learners that they got as much out of it as they did. Adding demonstration let me back into the discussion. Not to tell the learners how to do it, but to share with them authentically how I think about it.  I make space for them first, as I prefer if they're demonstrating to each other, but I watch and assess for when they need demonstration as a support.

The conditions that make engagement more likely are:

• Expectations. This goes hand in hand with the Equity Principle from the NCTM, which is near and dear to me. I believe all people can do significant, important mathematics. I really do. I try hard to communicate this to my learners.
• Responsibility. Learners make their own decisions about when, how and what to learn. THIS IS ANARCHY. I know. It's dangerous, especially when our learners have been trained for dependence and helplessness. Most students are not ready for full freedom immediately, but it is my goal for all of them. It's also my ongoing struggle to get students to understand that I both mean this and it doesn't mean that work is optional.
• Employment.  Learners need time to try out their learning in authentic situations. This connects with real life mathematics, with project based learning, with discovery learning and more. The students need to be the ones working if they are to be the ones learning.
• Approximation.  Learners need to be able to make mistakes without fear of punishment. If there's one area that math has completely screwed up on in the past, it is this. I do it, now you do it perfectly. This is crazy. We all know that no one learns anything important this way. And that the mistakes people make are crucial for learning in the first place.
• Response. Learners need real and meaningful feedback about what they are interested in working on. I now have my students put stickies on any work they turn in with what questions they have for me. Cambourne: "response must be relevant, appropriate, timely, readily available and nonthreatening." Grades are not feedback in this sense, and can only strive to be timely and readily available. (Although that does make grades better so far as it goes.)

Though I have made progress in creating the conditions, I have a long way to go.  (Although that implies an end to the journey and there may not be one.) They help determine what I teach, what my classroom is like, what I want to know about the students and their learning and how I evaluate their work.  That I would not have found them without colleagues in my professional learning community speaks to the heart of why that is important. So thank you, to Sue, Dave and Kathy, for helping me get this far.

While we did this as a teacher prep activity, I think it would be interesting with K-12 students as well. I first heard about anchor charts in Mosaic of Thought (I think), and like how they serve as both assessment and culture building. I've had students make charts about a particular concept, about what to do when you're stuck, and for what it means to do, learn and teach mathematics.

For this most recent lesson I had the students read "Mind mapping As a Tool in Mathematics Education", by Astrid Brinkman from Mathematics Teacher, Feb 2003. (They had previously expressed curiosity about and a lack of experience with concept maps.) One reason I love these is that they are frequently surprising. I expect one like this, that echoes the NCTM process standards we emphasize in the first unit: (Remember you can click images to see them full size.)

But then they go and make these completely original things like:
with different processes emphasized
Instructions to the students:

Activity: Anchor Charts
The following example comes from Ellin Keene’s (2008) To Understand: "Teachers generate anchor charts to capture and celebrate increasing sophistication in oral language use." (p. 278)
If you substitute ‘understanding learning in mathematics’ for ‘oral language use,’ you have the purpose of this activity. (Follow a link for a free pdf of the first chapter, under samples.)

Create an Anchor Chart for Learning in Mathematics
1. Identify the concepts and ideas that you want to remember as they relate to doing mathematics.
2. Develop an anchor chart that captures and celebrates your increasing sophistication in understanding “Doing Mathematics.” This might be a list, or a mind map, or a representation of your own creation. You decide – just be prepared to share your chart during our next class.
3. Be sure you leave 10 minutes to reflect.

Reflection: How well does your group’s anchor chart capture what you want your future students to think of hen you ask them “what does it mean to do mathematics?”


Home Extension: You might want to check out how math teachers use anchor charts at books.google.com - Integrating Literacy and Math. by Ellen Fogelberg, Carole Skalinder, Patti Satz, Barbara Hiller, and Lisa Bernstein.

Other interesting examples:

Send me yours or your students' and I would be happy to post that!