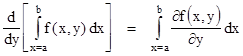|
Leibniz's Rule |
|
|
|
If� f(x,y)� is a well-behaved bi-variate function within the rectangle a<x<b, c<y<d, then we have |
|
|
|
|
|
This useful formula, known as Leibniz's Rule, is essentially just an application of the fundamental theorem of calculus.� To prove this rule, we can simply expand the differentiations on both sides as follows |
|
|
|
|
|
|
|
in the limit as the real number ε approaches zero.� Multiplying through by ε and distributing the integration on the right hand side, we see immediately that the equality holds. |
|
|
|
In a sense, Leibniz's Rule just expresses the fact that integration and differentiation are, in a sense, commutative.� This can be seen more clearly if we define the operators (for any fixed constants a,b) |
|
|
|
|
|
Leibniz's Rule asserts the commutativity of these operators, i.e., we have |
|
|
|
DyIx� =� IxDy |
|
|
|
For an example of how this rule is used, see Differential Operators and the Divergence Theorem. |
|
|