2010 PSLE Mathematics Seminar for Parents
Download as pptx, pdf2 likes979 views
Seminar for Parents Fairfield Methodist Primary School & Griffiths Primary School 26 & 27 February 2010
1 of 57
Downloaded 157 times

























































Ad
Recommended
Helping Students with PSLE Mathematics_6 February 2010



Helping Students with PSLE Mathematics_6 February 2010Jimmy Keng The document summarizes key points from a seminar for parents and tutors on helping students with Primary School Leaving Examination (PSLE) mathematics. It discusses the format and content of the PSLE math papers, including the introduction of calculators for Paper 2. It also reports on parents being upset over the perceived difficulty of this year's PSLE math paper due to more complex questions involving more steps and values as a result of allowing calculator use.
Henry Park PSLE Seminar for Parents



Henry Park PSLE Seminar for ParentsJimmy Keng This seminar for parents discussed the five key competencies in mathematical problem solving. Parental involvement is an important aspect of helping kids do well in school.
A Seminar for Parents Helping Your Child Prepare for PSLE Mathematics



A Seminar for Parents Helping Your Child Prepare for PSLE Mathematicsmathz4kidz Learning Centre The document summarizes key points from a seminar for parents on helping children prepare for the PSLE mathematics exam in Singapore. It provides examples of math problems and explains the level of working expected from different primary grades. It emphasizes the development of mathematical problem solving and visualization skills.
Lower Primary Maths Problem Solving



Lower Primary Maths Problem SolvingJimmy Keng The document discusses various problem solving heuristics for lower primary mathematics. It provides 14 examples of word problems demonstrating different heuristics students can use to solve problems, such as using tables, looking for patterns, guess and check, and breaking problems into steps. The heuristics allow students to systematically solve problems even if they are initially unfamiliar.
Parents Seminar on Heuristics at Chongfu School



Parents Seminar on Heuristics at Chongfu SchoolJimmy Keng This is the set of slides used at the seminar for Primary Five parents at Chongfu School in March 2011.
Parents Seminar on PSLE Mathematics



Parents Seminar on PSLE MathematicsJimmy Keng Here are some tips for improving problem solving skills in PSLE Mathematics:
- Take time to understand the question fully before attempting to solve it. Re-read if needed.
- Look for key information like numbers, operations, shapes etc and think about how they might be related.
- Draw diagrams or make lists when working with multiple steps, relationships or parts. This helps organize your thinking.
- Estimate answers before calculating to check if your working makes sense.
- Check your work - go back and ensure steps are correct and you have not made computational errors.
- Practice explaining your reasoning and showing your working, as this helps develop logical thinking skills.
- Review incorrect or challenging questions again later
Numeracy Oct 23 -Denise Flick



Numeracy Oct 23 -Denise FlickSchool District #20 Today's agenda includes a math lesson covering personal strategies for addition, subtraction, multiplication, and division. The schedule also includes a nutrition break, looking at virtual manipulatives and resources, lunch, and an assessment period. The document discusses teaching math concepts conceptually rather than procedurally and the importance of understanding operations rather than just memorizing computations. It provides examples of story problems and strategies adults use to solve math problems informally in everyday life.
8 step model drawing



8 step model drawingSitiIshak7 This document provides an overview of the 8-step model drawing strategy used in Singapore Math to help students solve word problems. It explains that model drawing is a key strategy that uses bars or diagrams to represent quantities in word problems visually. It then demonstrates how to set up and solve a variety of word problems using the 8-step model drawing approach through worked examples. The examples cover topics like addition, subtraction, fractions, ratios, percentages and more.
G6 m1-a-lesson 6-t



G6 m1-a-lesson 6-tmlabuski This document provides a lesson on solving ratio problems by finding equivalent ratios. It includes an example problem using tape diagrams to model ratios before and after a change. Students then work in groups on multiple practice problems involving ratios that change between situations. The lesson emphasizes drawing separate tape diagrams to visualize the ratios and quantities before and after a change occurs.
Minilessons for math_practice_g3-5



Minilessons for math_practice_g3-5Dania493634 This document provides an overview of the book "Minilessons for Math Practice, Grades 3–5" by Rusty Bresser and Caren Holtzman. The book presents 27 quick math activities that take 5-15 minutes and require little preparation. The activities are designed to provide practice for upper elementary students on key math concepts like number operations, algebra, geometry, data analysis, and measurement. Each activity includes instructions, questions for students, an example classroom scenario, and extension ideas. The goal is to broaden what it means to provide math practice and enhance students' understanding through applying skills in various problem-solving contexts throughout the school day.
MAV2013 Model Method



MAV2013 Model MethodJimmy Keng The document discusses the bar model method for teaching primary mathematics. It begins with an introduction to the presenter and includes links to additional resources. It then provides examples of using bar models to represent and solve word problems involving ratios, equations, and systems of equations. The examples are from primary classrooms in Singapore, New York, Chile, and Guatemala. The document demonstrates how bar models can help students learn abstract mathematical concepts through concrete, visual representations.
Book for word equations



Book for word equationsWYCLIFF AYONGA This document provides an introduction to 501 math word problems, a book designed to provide review and practice solving math problems. It contains 501 problems covering topics like fractions, decimals, percents, algebra, and geometry. The introduction explains how to use the book, with the problems organized into sections by math concept and complete answer explanations provided for each problem. It encourages readers to practice problems until they master the reasoning skills needed to solve similar problems in the future.
The Blake School's Seminar for Parents



The Blake School's Seminar for ParentsJimmy Keng The document is a slide presentation on mathematics learning in Singapore given by Yeap Ban Har from the Marshall Cavendish Institute in Singapore. It discusses Singapore's history of improving mathematics education over time, from achieving low passing rates on early exams to consistently high performance on international tests. It also describes Singapore's focus on visual and concrete learning approaches, as well as the country's emphasis on developing intellectual competence through mathematics.
Comparing Cards



Comparing CardsU1044470 The document describes an activity using comparing cards with images of owls to teach foundational numeracy concepts like more/less, ordering numbers, and number comparisons to early primary students. The activity involves students choosing cards, counting the owls, and determining which cards have more or less, then putting the cards in order from least to most. The goal is to establish thinking strategies around comparative language and numerical relationships.
Make Learning and Teaching Math Fun and Effective with Albert's Insomnia!



Make Learning and Teaching Math Fun and Effective with Albert's Insomnia!Rick Buchner Math classes from elementary schools report to us "a 23% increase in computational proficiency in just two weeks" and 33% more 3rd, 4th, and 5th grade students exceeding the state standard exam!
TEACH Academy 3-4 May 2013



TEACH Academy 3-4 May 2013Jimmy Keng - The document discusses teaching methods and philosophies around mathematics education in Singapore and the Philippines. It focuses on problem solving and critical thinking over rote memorization of content.
- Data is presented showing Singapore math students performing highly on international tests compared to other countries in Asia. The teaching approach emphasizes challenging word problems and real-world applications of mathematical concepts like area and volume.
- An example case study is provided showing how to solve problems calculating area and volume. A multi-step word problem involving money is also presented as an example of challenging problem solving.
Ten Frames



Ten Framesjwalts Ten-frames are useful tools for developing number sense in young children. They help visualize numbers in a way that is compatible with the base-ten number system. Research shows that ten-frames allow children to subitize, or instantly recognize small numbers, and also promote composing and decomposing numbers. The document provides instructions and examples of games that can be played with ten-frames to help children practice number recognition and math skills in an engaging way.
RightStart™ Mathematics Strategies Handout



RightStart™ Mathematics Strategies Handoutrightstartmath This document discusses strategies for teaching children math concepts like addition, subtraction, and multiplication in a more visual and conceptual way rather than relying on rote memorization and flash cards. It recommends strategies like using part-whole circles to show the relationship between addition and subtraction, visualizing quantities with objects or fingers, and strategies for addition and subtraction facts like "making 10" or "going up" from the number being subtracted. The document emphasizes that understanding concepts is more important than memorization alone for building long-term retention and motivation to learn math.
Dyscalculia test revised



Dyscalculia test revisedjudyhanning Here are the missing numbers or symbols:
7 + 2 = 9
– 4 = -3
+ 3 = 9 + 6
4 + 5 = 9
5 = 10
+ 6 = 11
= 7 + 3 = 10
3 = 8 - 5
= 16 - 10
– 6 = 10 - 6
2 = 6 + 4
5 = 11 - 6
This task examines the student’s understanding of basic addition, subtraction, and order of
operations. Younger students may not understand all of the concepts.
24
Use the symbols to perform the math problems.
= +3 9
= –1 5
1st Grade Math Activity: Golden Hexagon (Algebra)



1st Grade Math Activity: Golden Hexagon (Algebra)Mango Math Group A sample math lesson from Mango Math's First grade math curriculum.
Mango Math provides grade level math games and activities that reinforce core math concepts. Our activities are designed to enhance and compliment existing curriculum and are aligned with NCTM standards. Our innovative and fun math curriculum products are designed to assist teachers, resource room instructors, home school organizations, and parents build positive attitudes towards math while reinforcing key math skills.
for more information visit www.mangomathgroup.com
Debunking misconceptions about mathematics in the early years



Debunking misconceptions about mathematics in the early yearsThe Australian Association of Mathematics Teachers (AAMT) Inc. Debunking misconceptions about mathematics in the early years is the first of a four part series of Connect with Maths webinars
Kim freeman mighty math for 4-6 year olds introducing addition and subtraction



Kim freeman mighty math for 4-6 year olds introducing addition and subtractionДимитричка Апостолова This document is the table of contents and introduction for the book "Mighty Math, Beginner Mathematician Book 3, Introducing Addition and Subtraction". The book teaches 4-6 year olds the arithmetic operations of addition and subtraction through fun activities and the use of number lines. It aims to increase children's confidence in dealing with numbers and arithmetic. The Mighty Math series provides a structured approach to learning mathematics at a beginner level through colorful, engaging books.
Kim freeman mighty math for 4-6 year olds introducing multiplication and div...



Kim freeman mighty math for 4-6 year olds introducing multiplication and div...Димитричка Апостолова This document provides information about a series of mathematics books for children ages 4-7, including Book 4 which focuses on introducing multiplication and division concepts. It discusses key topics covered in each book, such as numbers, arithmetic operations, and fractions. The series is designed to develop children's mathematical skills in a structured way through fun activities.
Worcester State University Summer Institute Lecture 1



Worcester State University Summer Institute Lecture 1Jimmy Keng Day 1 Plenary Lecture on a selection of learning theories that underpin Singapore Math. The focus is on Bruner's theories with mentions of Dienes and Skemp.
Kim Freeman-Mighty math for 4-6 Year Olds_ Introducing Mathematics



Kim Freeman-Mighty math for 4-6 Year Olds_ Introducing MathematicsДимитричка Апостолова This document is an excerpt from a book that teaches early mathematics to children ages 4-6. It includes instructions for parents on how to help their children with math as well as math exercises involving counting, number recognition, and comparisons of quantity. The full book teaches concepts like counting from 1 to 10, writing numbers, ordering numbers, and basic arithmetic operations.
Repeated addition hands on



Repeated addition hands onchamberlainc This is a keynote for teaching 3rd graders how to process multiplication using repeated addition. There is a video, from Discovery Education, included in the presentation.
Maths seminar i (1)



Maths seminar i (1)drselvarani This document provides biographical details about the mathematician Srinivasa Ramanujan in 3 sections. It outlines his early life and education in India, his collaboration with G.H. Hardy at Trinity College Cambridge from 1914-1919, and highlights some of his seminal contributions to mathematical constants, infinite series, and continued fractions. These include his formulas for computing pi to many decimal places and redefining Euler's constant. The document also mentions some of Ramanujan's mentors and the applications his work has found in fields like physics, computer science, and engineering.
Speed time distance



Speed time distancerajeshb1980 1. The document provides teaching notes on speed, time, and distance concepts including definitions of key terms like speed, average speed, and relative speed.
2. It includes examples of speed, time, and distance word problems and step-by-step solutions showing calculations and conversions between units.
3. Sample problems cover topics like calculating time to meeting points, average speeds, relative speeds of objects traveling in the same or opposite directions, and speed of boats traveling upstream or downstream.
Unit 2



Unit 2Sashri Lisdiani This document provides an overview of key concepts related to kinematics including distance, time, speed, velocity, acceleration, and free fall. It begins by defining speed and describing how to calculate average speed. It then discusses velocity and acceleration, explaining how to calculate changes in velocity and acceleration. Graphs of distance-time, speed-time and their interpretations are presented. The document concludes by discussing Galileo's discovery of the acceleration of free fall and how air resistance affects falling objects.
Ict Maths Fil Images Jan2010



Ict Maths Fil Images Jan2010lsoliverpool Some minor outputs. Major outputs are in the direction of use of technology to make learning more interactive and pleasurable. Impact assessment is growing.
Ad
More Related Content
What's hot (18)
G6 m1-a-lesson 6-t



G6 m1-a-lesson 6-tmlabuski This document provides a lesson on solving ratio problems by finding equivalent ratios. It includes an example problem using tape diagrams to model ratios before and after a change. Students then work in groups on multiple practice problems involving ratios that change between situations. The lesson emphasizes drawing separate tape diagrams to visualize the ratios and quantities before and after a change occurs.
Minilessons for math_practice_g3-5



Minilessons for math_practice_g3-5Dania493634 This document provides an overview of the book "Minilessons for Math Practice, Grades 3–5" by Rusty Bresser and Caren Holtzman. The book presents 27 quick math activities that take 5-15 minutes and require little preparation. The activities are designed to provide practice for upper elementary students on key math concepts like number operations, algebra, geometry, data analysis, and measurement. Each activity includes instructions, questions for students, an example classroom scenario, and extension ideas. The goal is to broaden what it means to provide math practice and enhance students' understanding through applying skills in various problem-solving contexts throughout the school day.
MAV2013 Model Method



MAV2013 Model MethodJimmy Keng The document discusses the bar model method for teaching primary mathematics. It begins with an introduction to the presenter and includes links to additional resources. It then provides examples of using bar models to represent and solve word problems involving ratios, equations, and systems of equations. The examples are from primary classrooms in Singapore, New York, Chile, and Guatemala. The document demonstrates how bar models can help students learn abstract mathematical concepts through concrete, visual representations.
Book for word equations



Book for word equationsWYCLIFF AYONGA This document provides an introduction to 501 math word problems, a book designed to provide review and practice solving math problems. It contains 501 problems covering topics like fractions, decimals, percents, algebra, and geometry. The introduction explains how to use the book, with the problems organized into sections by math concept and complete answer explanations provided for each problem. It encourages readers to practice problems until they master the reasoning skills needed to solve similar problems in the future.
The Blake School's Seminar for Parents



The Blake School's Seminar for ParentsJimmy Keng The document is a slide presentation on mathematics learning in Singapore given by Yeap Ban Har from the Marshall Cavendish Institute in Singapore. It discusses Singapore's history of improving mathematics education over time, from achieving low passing rates on early exams to consistently high performance on international tests. It also describes Singapore's focus on visual and concrete learning approaches, as well as the country's emphasis on developing intellectual competence through mathematics.
Comparing Cards



Comparing CardsU1044470 The document describes an activity using comparing cards with images of owls to teach foundational numeracy concepts like more/less, ordering numbers, and number comparisons to early primary students. The activity involves students choosing cards, counting the owls, and determining which cards have more or less, then putting the cards in order from least to most. The goal is to establish thinking strategies around comparative language and numerical relationships.
Make Learning and Teaching Math Fun and Effective with Albert's Insomnia!



Make Learning and Teaching Math Fun and Effective with Albert's Insomnia!Rick Buchner Math classes from elementary schools report to us "a 23% increase in computational proficiency in just two weeks" and 33% more 3rd, 4th, and 5th grade students exceeding the state standard exam!
TEACH Academy 3-4 May 2013



TEACH Academy 3-4 May 2013Jimmy Keng - The document discusses teaching methods and philosophies around mathematics education in Singapore and the Philippines. It focuses on problem solving and critical thinking over rote memorization of content.
- Data is presented showing Singapore math students performing highly on international tests compared to other countries in Asia. The teaching approach emphasizes challenging word problems and real-world applications of mathematical concepts like area and volume.
- An example case study is provided showing how to solve problems calculating area and volume. A multi-step word problem involving money is also presented as an example of challenging problem solving.
Ten Frames



Ten Framesjwalts Ten-frames are useful tools for developing number sense in young children. They help visualize numbers in a way that is compatible with the base-ten number system. Research shows that ten-frames allow children to subitize, or instantly recognize small numbers, and also promote composing and decomposing numbers. The document provides instructions and examples of games that can be played with ten-frames to help children practice number recognition and math skills in an engaging way.
RightStart™ Mathematics Strategies Handout



RightStart™ Mathematics Strategies Handoutrightstartmath This document discusses strategies for teaching children math concepts like addition, subtraction, and multiplication in a more visual and conceptual way rather than relying on rote memorization and flash cards. It recommends strategies like using part-whole circles to show the relationship between addition and subtraction, visualizing quantities with objects or fingers, and strategies for addition and subtraction facts like "making 10" or "going up" from the number being subtracted. The document emphasizes that understanding concepts is more important than memorization alone for building long-term retention and motivation to learn math.
Dyscalculia test revised



Dyscalculia test revisedjudyhanning Here are the missing numbers or symbols:
7 + 2 = 9
– 4 = -3
+ 3 = 9 + 6
4 + 5 = 9
5 = 10
+ 6 = 11
= 7 + 3 = 10
3 = 8 - 5
= 16 - 10
– 6 = 10 - 6
2 = 6 + 4
5 = 11 - 6
This task examines the student’s understanding of basic addition, subtraction, and order of
operations. Younger students may not understand all of the concepts.
24
Use the symbols to perform the math problems.
= +3 9
= –1 5
1st Grade Math Activity: Golden Hexagon (Algebra)



1st Grade Math Activity: Golden Hexagon (Algebra)Mango Math Group A sample math lesson from Mango Math's First grade math curriculum.
Mango Math provides grade level math games and activities that reinforce core math concepts. Our activities are designed to enhance and compliment existing curriculum and are aligned with NCTM standards. Our innovative and fun math curriculum products are designed to assist teachers, resource room instructors, home school organizations, and parents build positive attitudes towards math while reinforcing key math skills.
for more information visit www.mangomathgroup.com
Debunking misconceptions about mathematics in the early years



Debunking misconceptions about mathematics in the early yearsThe Australian Association of Mathematics Teachers (AAMT) Inc. Debunking misconceptions about mathematics in the early years is the first of a four part series of Connect with Maths webinars
Kim freeman mighty math for 4-6 year olds introducing addition and subtraction



Kim freeman mighty math for 4-6 year olds introducing addition and subtractionДимитричка Апостолова This document is the table of contents and introduction for the book "Mighty Math, Beginner Mathematician Book 3, Introducing Addition and Subtraction". The book teaches 4-6 year olds the arithmetic operations of addition and subtraction through fun activities and the use of number lines. It aims to increase children's confidence in dealing with numbers and arithmetic. The Mighty Math series provides a structured approach to learning mathematics at a beginner level through colorful, engaging books.
Kim freeman mighty math for 4-6 year olds introducing multiplication and div...



Kim freeman mighty math for 4-6 year olds introducing multiplication and div...Димитричка Апостолова This document provides information about a series of mathematics books for children ages 4-7, including Book 4 which focuses on introducing multiplication and division concepts. It discusses key topics covered in each book, such as numbers, arithmetic operations, and fractions. The series is designed to develop children's mathematical skills in a structured way through fun activities.
Worcester State University Summer Institute Lecture 1



Worcester State University Summer Institute Lecture 1Jimmy Keng Day 1 Plenary Lecture on a selection of learning theories that underpin Singapore Math. The focus is on Bruner's theories with mentions of Dienes and Skemp.
Kim Freeman-Mighty math for 4-6 Year Olds_ Introducing Mathematics



Kim Freeman-Mighty math for 4-6 Year Olds_ Introducing MathematicsДимитричка Апостолова This document is an excerpt from a book that teaches early mathematics to children ages 4-6. It includes instructions for parents on how to help their children with math as well as math exercises involving counting, number recognition, and comparisons of quantity. The full book teaches concepts like counting from 1 to 10, writing numbers, ordering numbers, and basic arithmetic operations.
Repeated addition hands on



Repeated addition hands onchamberlainc This is a keynote for teaching 3rd graders how to process multiplication using repeated addition. There is a video, from Discovery Education, included in the presentation.
Debunking misconceptions about mathematics in the early years



Debunking misconceptions about mathematics in the early yearsThe Australian Association of Mathematics Teachers (AAMT) Inc.
Kim freeman mighty math for 4-6 year olds introducing multiplication and div...



Kim freeman mighty math for 4-6 year olds introducing multiplication and div...Димитричка Апостолова
Viewers also liked (14)
Maths seminar i (1)



Maths seminar i (1)drselvarani This document provides biographical details about the mathematician Srinivasa Ramanujan in 3 sections. It outlines his early life and education in India, his collaboration with G.H. Hardy at Trinity College Cambridge from 1914-1919, and highlights some of his seminal contributions to mathematical constants, infinite series, and continued fractions. These include his formulas for computing pi to many decimal places and redefining Euler's constant. The document also mentions some of Ramanujan's mentors and the applications his work has found in fields like physics, computer science, and engineering.
Speed time distance



Speed time distancerajeshb1980 1. The document provides teaching notes on speed, time, and distance concepts including definitions of key terms like speed, average speed, and relative speed.
2. It includes examples of speed, time, and distance word problems and step-by-step solutions showing calculations and conversions between units.
3. Sample problems cover topics like calculating time to meeting points, average speeds, relative speeds of objects traveling in the same or opposite directions, and speed of boats traveling upstream or downstream.
Unit 2



Unit 2Sashri Lisdiani This document provides an overview of key concepts related to kinematics including distance, time, speed, velocity, acceleration, and free fall. It begins by defining speed and describing how to calculate average speed. It then discusses velocity and acceleration, explaining how to calculate changes in velocity and acceleration. Graphs of distance-time, speed-time and their interpretations are presented. The document concludes by discussing Galileo's discovery of the acceleration of free fall and how air resistance affects falling objects.
Ict Maths Fil Images Jan2010



Ict Maths Fil Images Jan2010lsoliverpool Some minor outputs. Major outputs are in the direction of use of technology to make learning more interactive and pleasurable. Impact assessment is growing.
Time Speed & Distance basics



Time Speed & Distance basicsRajesh Singh Time Speed & Distance(TSD) questions are necessarily part of all Quantitative aptitude test. This Presentation is easy and unique approach to understand concept of TSD. Its various application and types of questions are also explained.Learn simple solutions of some difficult questions of TSD- https://www.youtube.com/watch?v=nAeerBmX_Tc
Pre calculus intro- 2013



Pre calculus intro- 2013Ron Eick This document contains information about Mr. Eick's pre-calculus class, including an overview of topics to be covered, grading policies, required materials, classroom rules and procedures. The main topics to be covered are functions, transformations, complex numbers, rational functions, exponential and logarithmic functions, trigonometry, vectors, systems of equations/matrices, sequences, series and probability. Tests, quizzes, homework, projects and class participation will be graded. Students are expected to bring their notebook, calculator and pencils to each class and follow rules about tardiness, electronic devices, respecting others and school property.
Speed, time, distance



Speed, time, distancetracyconover Motion refers to an object changing position over time relative to a reference point. Speed is the distance an object travels divided by the time taken and is measured in meters per second or kilometers per hour. Average speed is the total distance divided by the total time. Velocity also includes direction of motion. Acceleration is the rate at which velocity changes. A force is a push or pull measured in newtons, but a force being applied does not necessarily mean motion will occur. The net force is the combination of all acting forces on an object. Gravity is the force of attraction between objects due to their mass. Weight is a measure of the gravitational force on an object that depends on its mass and ___location.
Time distance



Time distancevangielyn This document provides information about time, distance, and speed including key concepts, units of measurement, conversion formulas between units, and formulas to calculate distance, time, and speed given two of the three variables. It includes examples of using the formulas to solve word problems involving trains passing poles and travel between cities. The document emphasizes that speed, time, and distance are important concepts in navigation, athletics, and transportation scheduling.
Chapter 4



Chapter 4Caroline Chua The document summarizes factors that led to Hitler's rise to power in Germany in the 1930s. The Weimar government was unpopular due to economic struggles following World War 1. Hitler gained support by promising to restore Germany's power and overturn the Treaty of Versailles. He took advantage of the weaknesses of the Weimar government and fears of communism. Through his charismatic speaking and reorganization of the Nazi party, Hitler was able to rise to power and become Chancellor of Germany in 1933.
Sample Documentation Report 03.11.09



Sample Documentation Report 03.11.09pccampo This document describes an action plan for a waste segregation project in the GK Elizabeth Seton 1N-Y community. It includes a community profile, background on the need for the project based on a community assessment, objectives and activities, a schedule, assignments, resources, expenses, results and an evaluation. The project aimed to educate community members on proper waste segregation through workshops and a clean-up activity over four Saturdays to improve solid waste management in the area.
Bring Your Textbook to Life! Ideas & Resources



Bring Your Textbook to Life! Ideas & ResourcesShelly Sanchez Terrell This document provides many strategies, tips, and technology tools for bringing textbooks to life and making textbook content more engaging for students. It suggests deconstructing textbooks into their key elements like exercises, assessments, examples, vocabulary and visuals. It also recommends sketchnoting, using social bookmarking tools to curate content, creating graphic organizers, games, infographics, timelines, comics, and digital stories. Additionally, it lists ideas for virtual field trips, audio projects, video projects, and augmented reality tools to enhance textbook learning. All of the tips and technologies are aimed at helping students better understand and interact with textbook material.
Pass That Exam! Test Prep Strategies & Resources



Pass That Exam! Test Prep Strategies & ResourcesShelly Sanchez Terrell My books- Learning to Go https://gumroad.com/l/learn2go & The 30 Goals Challenge for Teachers http://amazon.com/The-Goals-Challenge-Teachers-Transform/dp/0415735343
Resources at http://shellyterrell.com/assessment & http://shellyterrell.com/examprep
Speed Time Distance - C1



Speed Time Distance - C12IIM B runs diagonally across a square while A runs along the sides, traveling a total of 20 meters. Given that originally B reached the endpoint 2 seconds after A, and with double the speed B would reach it 2 seconds before A, the solution shows that B's original speed is approximately equal to 1.75 m/s.
Sample seminar report



Sample seminar reportFarman Khan The document provides guidelines for writing a seminar report, including formatting instructions for aspects like page dimensions, binding specifications, font styles, and report section order and content. Key sections should include an abstract, table of contents, chapters on the topic's introduction, literature review and conclusions, and a references list. Appendices can include supplementary information. Headings, tables and figures must correspond to the referenced text.
Ad
Similar to 2010 PSLE Mathematics Seminar for Parents (20)
Helping Students with PSLE Mathematics_6 February 2010



Helping Students with PSLE Mathematics_6 February 2010Jimmy Keng A Seminar for Parents & Tutors
Helping Students with
PSLE Mathematics
6 February 2010
SINGAPOTE TEACHERS’ UNION
Yeap Ban Har
National Institute of Education
Nanyang Technological University
Singapore
How to Ace PSLE Maths



How to Ace PSLE MathsJimmy Keng The document provides information about preparing for and taking the PSLE Mathematics exam in Singapore. It discusses the structure of the exam, which consists of two papers, and outlines the curriculum focus on problem solving. It also provides examples of different types of math problems students may encounter on the exam. At the end, it discusses a news article where parents complained that this year's PSLE math exam was unusually difficult, possibly because it was the first year calculators were allowed.
2010 Henry Park Primary School Seminar for Parents



2010 Henry Park Primary School Seminar for ParentsJimmy Keng This document summarizes a seminar for parents about the PSLE mathematics exam. It discusses the exam format, which consists of two papers, and explains that the exam tests concepts covered in the primary school mathematics curriculum and problem-solving skills. It provides examples of different types of problems featured in the exam. The document emphasizes that mathematical problem-solving, visualization, number sense, self-monitoring of thinking, communication, and pattern recognition are important competencies tested in the exam. Textbooks and lessons in primary school aim to develop these skills in students.
Association of Mathematics Educators Seminar on PSLE Mathematics



Association of Mathematics Educators Seminar on PSLE MathematicsJimmy Keng This seminar was for parents and teachers interested in helping students in preparing for the PSLE Mathematics.
Bendermeer Primary School Seminar for Parents



Bendermeer Primary School Seminar for ParentsJimmy Keng This document provides an overview of a presentation on helping children with primary mathematics. It discusses how mathematics can develop intellectual competence and reflects on shifts in test questions to require more conceptual understanding and real-world problem solving over rote algorithms. Examples of math questions and lessons from various primary grades in Singapore, the US, UK, Netherlands and Japan are presented, covering topics like number sense, patterns, problem solving and visual models. Key competencies and strategies for problem solving are discussed.
Ryedale School - Aspire and Achieve Year 7 



Ryedale School - Aspire and Achieve Year 7 Gareth Jenkins Students in year 7 have opportunities to get involved in extracurricular activities before and after school as well as during lunchtimes. These include sports clubs, arts clubs, homework clubs and subject-specific clubs. Participating in clubs and activities helps students develop a thirst for knowledge and be happy participants in school life. Parents are encouraged to support their child's learning by discussing clubs they could join and helping them get involved.
AME PSLE Seminar



AME PSLE SeminarJimmy Keng PSLE Mathematics Seminar
Association of Mathematics Educators
Dr. Yeap Ban Har
National Institute of Education
Nanyang Technological University
This seminar was conducted at Singapore Polytechnic.
Mahasarakham Rajabhat University Day 1



Mahasarakham Rajabhat University Day 1Jimmy Keng Rajabhat Mahasarakham organised this workshop titled Transforming the Mathematics Classroom. The goal is to get teachers to think about teaching mathematics to encourage thinking, to develop visualization and to enhance the ability to observe patterns rather than mathematics as a subject that requires memorization, carrying out meaningless procedures and doing tedious computations.
[myPITA] Multiplication -- More Than Repeated Addition and Times Tables.pdf![[myPITA] Multiplication -- More Than Repeated Addition and Times Tables.pdf](https://cdn.slidesharecdn.com/ss_thumbnails/mypitamultiplication-morethanrepeatedadditionandtimestables-250414175625-0d454b02-thumbnail.jpg?width=560&fit=bounds)
![[myPITA] Multiplication -- More Than Repeated Addition and Times Tables.pdf](https://cdn.slidesharecdn.com/ss_thumbnails/mypitamultiplication-morethanrepeatedadditionandtimestables-250414175625-0d454b02-thumbnail.jpg?width=560&fit=bounds)
![[myPITA] Multiplication -- More Than Repeated Addition and Times Tables.pdf](https://cdn.slidesharecdn.com/ss_thumbnails/mypitamultiplication-morethanrepeatedadditionandtimestables-250414175625-0d454b02-thumbnail.jpg?width=560&fit=bounds)
![[myPITA] Multiplication -- More Than Repeated Addition and Times Tables.pdf](https://cdn.slidesharecdn.com/ss_thumbnails/mypitamultiplication-morethanrepeatedadditionandtimestables-250414175625-0d454b02-thumbnail.jpg?width=560&fit=bounds)
[myPITA] Multiplication -- More Than Repeated Addition and Times Tables.pdfChris Hunter Multiplication is repeated addition... but it also means so much more than that! In this workshop, you will explore several fundamental meanings of this operation (e.g., equal groups, arrays and areas, how a quantity is “stretched,” etc.) through rich tasks that address each of these meanings. Also, you will explore and discuss relationships between the “basic facts.” More importantly, you will learn how to help your students see that these relationships extend to other types of numbers that they come across in BC’s intermediate and middle years mathematics curriculum (e.g., two-digit whole numbers, fractions, decimals, integers, etc.).
International School Saigon Pearl



International School Saigon PearlJimmy Keng This document summarizes a seminar on the Singapore Math approach. It discusses key concepts like conceptual understanding, variation theory, concrete-pictorial-abstract instruction, and assessment results that show Singapore student performance. Example word problems are provided to illustrate how Singapore Math teaches for understanding over rote memorization.
Addition Detective



Addition DetectiveNicole Pilarz This lesson plan introduces first grade students to math mountains as a way to find unknown partners in addition equations. The lesson will have students:
1. Learn that math mountains show the total and two partners, and that switching partners does not change the total.
2. Practice finding missing totals and partners in math mountains by counting on with circles or fingers.
3. Play a game called "Addition Detective" in groups to further practice these skills.
4. Take the game home to teach their families and continue practicing unknown partners.
Maths evening 2018



Maths evening 2018Sandygate This document provides information from a Maths Information Evening for parents. It discusses what progress in maths entails, how maths is taught in key stages 1 and 2, and different maths concepts covered, including place value, addition, subtraction, multiplication, division, and problem solving. Parents are advised to praise their children's efforts, play maths games at home, and focus on building confidence rather than stressing workbooks or written methods.
Math stars grade 4



Math stars grade 4anilaraju The document contains a collection of math word problems and exercises for students. It includes problems involving geometry, algebra, time, money, fractions, probability and other topics. After each problem section, it provides the answers and an explanation of the problem solving strategies and concepts involved. The purpose is to challenge students with complex multi-step problems and help them improve their problem solving skills.
Developing Critical Thinking Through Singapore Math



Developing Critical Thinking Through Singapore MathJimmy Keng Yeap Ban Har gave this repeat seminar at Keys Grade School to teachers from Filipino schools and parents.
Interim 1 Review



Interim 1 ReviewLauren Pressley The document contains multiple math word problems and questions. It asks the reader to evaluate expressions, find missing values, draw graphs, choose the student with the correct solution, write equations, and determine which variable had the least variation from data. It also provides tables with numbers and asks questions about the data.
AMATYC Ignite 2017 1st Half



AMATYC Ignite 2017 1st HalfFred Feldon This document provides information about the Student Research League (SRL) competition. The SRL is a mathematical research competition for two-year college students held each spring. Students have nine days to research and solve a challenge problem with a faculty mentor. Problems relate to real-world issues and require mathematical modeling. Components of the competition include the challenge problem, career research, a mathematical model or thesis, and a thesis defense. Prizes include a $1,500 grand prize. The goal is to encourage mathematical problem solving and provide an outlet for two-year college students to compete in research contests.
Outreach p6-math@



Outreach p6-math@Azis Ibrahim 1. The document is about a book titled "Primary 6 Mathematics Ace The Exams with My 24/7 Personal Tutor" which contains 10 mock exam papers and detailed explanations for Primary 6 math questions on a CD-ROM.
2. The book is meant to help pupils prepare for Primary 6 math exams by including exam-style questions that highlight common misconceptions.
3. The accompanying CD-ROM contains video lessons explaining how to solve each question in the mock exams.
Outreach p6-math.#



Outreach p6-math.#Azis Ibrahim 1. The document is about a book titled "Primary 6 Mathematics Ace The Exams with My 24/7 Personal Tutor" which contains 10 mock exam papers and detailed explanations for Primary 6 math questions on a CD-ROM.
2. The book is intended to help pupils prepare for Primary 6 math exams by including exam-style questions that highlight common misconceptions.
3. The accompanying CD-ROM contains video lessons explaining the solutions to each question in the mock exams.
3 problems



3 problemsJeff Smith The document discusses making math class more meaningful and engaging for students. It suggests that students hire teachers to help them make progress and have fun with friends, but that current math assignments like doing evens on page 276 do not achieve this. It proposes finding real-life problems as driving questions for math lessons instead, like issues around road safety, healthcare costs, or immigration. Students would research and develop deliverables like presentations or books to answer their chosen question. The goals are for students to get important work done, define themselves, and stay connected to others.
Raising Critical Thinkers Through Singapore Math Keys Grade School Manila Jan...



Raising Critical Thinkers Through Singapore Math Keys Grade School Manila Jan...Jimmy Keng Raising Critical Thinkers through Singapore Math (another email)
Keys Grade School, Manila, January 2010
Ad
More from Jimmy Keng (20)
Maths Hub June 2015 Day 1 and Day 2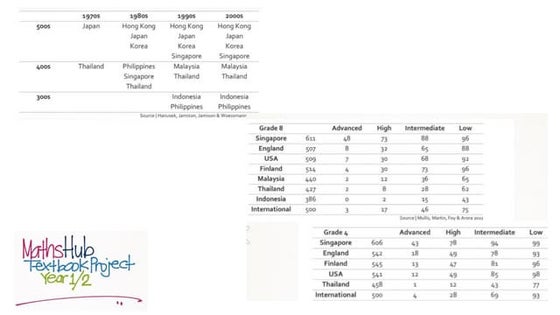



Maths Hub June 2015 Day 1 and Day 2Jimmy Keng This document discusses differentiating instruction to challenge advanced learners. It provides examples of ways to assess basic subtraction skills through runway indicators. For advanced learners, it suggests having them solve problems in alternative ways, write stories for equations, or write notes applying math concepts to enrich their learning beyond basic skills.
Math Plus Kansas City



Math Plus Kansas CityJimmy Keng The document discusses using math journals in elementary school classrooms to teach mathematical concepts. It describes a framework for teaching mastery that involves anchor tasks, guided practice, and independent practice. Journaling is presented as one part of this process where students explore concepts, structure their understanding, and reflect on their learning. Examples are provided of kindergarteners recording number bonds in their journals to master basic counting and addition. The journal entries allow teachers to assess understanding and provide differentiated instruction.
Primary Mathematics Fractions



Primary Mathematics FractionsJimmy Keng Basic Lesson Structure of Singapore Math - anchor task, guided practice and independent practice
Blake School Presentation Grade 1



Blake School Presentation Grade 1Jimmy Keng The document outlines a schedule for four sessions occurring between 08:30-04:00 with a forum period from 03:30-04:00. It then discusses using a lesson on the Common Core to understand critical areas for Grade 1, including number bonds, comparison of numbers, and conservation of numbers. Various methods for developing visualization like the CPA approach, bar models, and teacher questioning are listed. The document goes on to discuss elements of effective math lessons including exploration, structure, journaling, reflection, and guided/independent practice using addition and subtraction strategies like counting all, making 10, subtracting from ten, and renaming before subtracting with examples provided.
Blake Grade 6



Blake Grade 6Jimmy Keng This document provides an overview of a middle school mathematics institute that will take place on Saturday. It discusses the basic lesson format, which includes an anchor task, guided practice, and independent practice. It also references Bruner's idea of using concrete experiences and pictorial representations to help students understand abstract ideas. The document then provides several case studies as examples of lessons that could be used to develop, apply, and practice various mathematical concepts involving fractions, algebra, geometry, and more.
Blake grade 5



Blake grade 5Jimmy Keng This document provides an overview of a Grade 5 mathematics institute that will take place on a Friday. It outlines the basic lesson format, which includes an anchor task, guided practice, and independent practice. It also references several learning theories that provide a framework for the lesson, such as Bruner's idea of concrete, iconic, and symbolic representations. The document includes several math word problems from past PSLE exams in Singapore to use for practice. It concludes with key learning theories covered and strategies for challenging advanced learners.
Blake Grade 4



Blake Grade 4Jimmy Keng 1) The document discusses standards and instructional focus areas for Grade 4 mathematics, including multi-digit multiplication and division, fractions, and geometric shapes.
2) It provides examples of case studies to solve, including arranging fractions in order and word problems involving fractions of amounts.
3) Theories of learning and representation discussed include Bruner's CPA approach and Skemp's classifications of understanding in mathematics.
Blake Grade 3



Blake Grade 3Jimmy Keng This document provides information about a grade 3 mathematics institute to be held on Wednesday. It discusses key theories in mathematics learning from Piaget, Bruner, Dienes, Vygotsky, and Skemp. The document also provides several case studies with examples of lesson plans and problems that assess different mathematical concepts like operations, fractions, problem solving, and place value.
Blake Grade 2



Blake Grade 2Jimmy Keng The document discusses a Grade 2 math institute that will focus on place value using concrete and pictorial representations. It provides several case studies on topics like subtraction across zeros, fractions, and problem solving. The lessons follow a basic format of an anchor task, guided practice, and independent practice. Key learning theories that will be drawn from include those from Piaget, Bruner, Dienes, Vygotsky, and Skemp. Bruner's CPA approach and Skemp's classifications of understanding will be particularly relevant for using different representations to build conceptual and relational understanding.
Blake Grade 1



Blake Grade 1Jimmy Keng Participants to Blake School Singapore Math Institute in June 2015 please download and print this set of handouts.
2104 WSU Cutouts



2104 WSU CutoutsJimmy Keng This document contains instructions for cutting out numbers and mathematical symbols from a page. It includes numbers from 0 to 9, basic mathematical operators like + and -, and instructions to cut out the listed items. The document is repetitive, listing the same numbers and symbols twice.
2014 WSU Handouts



2014 WSU HandoutsJimmy Keng The document summarizes discussions from breakout sessions at the 4th Singapore Math Institute on teaching mathematics using Singapore's approach. It provides tasks and problems from Singapore classrooms related to practicing skills through problem-solving, using anchor tasks to structure lessons, and teaching geometry in grades 4-6. The goals are to emulate Singapore's emphasis on problem-solving and multi-step word problems to develop students' mathematical thinking.
2014 WSU Day 2



2014 WSU Day 2Jimmy Keng The document discusses strategies for developing and improving mathematical practices, such as using anchor tasks, collaborative structures, questioning techniques, journals, textbooks for reflection, and focusing on visualization, generalization, and number sense. It also discusses moving from concrete to pictorial to abstract representations, and using anchor tasks and challenging word problems to teach Singapore math concepts.
2014 WSU Day 1 Slides



2014 WSU Day 1 SlidesJimmy Keng This document discusses using a problem-solving approach to teach mathematics. It focuses on practicing problem-solving lessons and breaking students into groups to work on problems. The document provides resources for lesson plans and contact information for the speaker who advocates for integrating problem-solving into mathematics education.
Se01 abc's of singapore math through whole numbers



Se01 abc's of singapore math through whole numbersJimmy Keng The document discusses the Singapore approach to teaching mathematics, which was developed to help Singaporean students perform better in math. It is based on Bruner's ideas of a spiral curriculum and using representations. The document provides 15 sample math tasks that demonstrate fundamentals of Singapore Math instruction, such as the Concrete-Pictorial-Abstract approach. It also includes quotes from Bruner about revisiting basic ideas repeatedly to help students master structured bodies of knowledge.
Sd09 visualization



Sd09 visualizationJimmy Keng This document contains an agenda for a staff development conference on Singapore Math strategies with a focus on visualization. It includes 4 sample math tasks: 1) finding the area of a 4-sided polygon on a geoboard; 2) calculating leftover wire used to make a figure of 6 equilateral triangles; 3) dividing numbers by 3, 4, and 6; and 4) a word problem about Peter and Nancy exchanging coins to determine how many Peter originally had. The tasks are meant to illustrate ways to get students to visualize math concepts.
Recently uploaded (20)
What is the Philosophy of Statistics? (and how I was drawn to it)



What is the Philosophy of Statistics? (and how I was drawn to it)jemille6 What is the Philosophy of Statistics? (and how I was drawn to it)
Deborah G Mayo
At Dept of Philosophy, Virginia Tech
April 30, 2025
ABSTRACT: I give an introductory discussion of two key philosophical controversies in statistics in relation to today’s "replication crisis" in science: the role of probability, and the nature of evidence, in error-prone inference. I begin with a simple principle: We don’t have evidence for a claim C if little, if anything, has been done that would have found C false (or specifically flawed), even if it is. Along the way, I’ll sprinkle in some autobiographical reflections.
All About the 990 Unlocking Its Mysteries and Its Power.pdf



All About the 990 Unlocking Its Mysteries and Its Power.pdfTechSoup In this webinar, nonprofit CPA Gregg S. Bossen shares some of the mysteries of the 990, IRS requirements — which form to file (990N, 990EZ, 990PF, or 990), and what it says about your organization, and how to leverage it to make your organization shine.
2025 The Senior Landscape and SET plan preparations.pptx



2025 The Senior Landscape and SET plan preparations.pptxmansk2 2025 The Senior Landscape and SET plan preparations.pptx
antiquity of writing in ancient India- literary & archaeological evidence



antiquity of writing in ancient India- literary & archaeological evidencePrachiSontakke5 for the students of BA Sem
History Of The Monastery Of Mor Gabriel Philoxenos Yuhanon Dolabani



History Of The Monastery Of Mor Gabriel Philoxenos Yuhanon Dolabanifruinkamel7m History Of The Monastery Of Mor Gabriel Philoxenos Yuhanon Dolabani
History Of The Monastery Of Mor Gabriel Philoxenos Yuhanon Dolabani
History Of The Monastery Of Mor Gabriel Philoxenos Yuhanon Dolabani
Ancient Stone Sculptures of India: As a Source of Indian History



Ancient Stone Sculptures of India: As a Source of Indian HistoryVirag Sontakke This Presentation is prepared for Graduate Students. A presentation that provides basic information about the topic. Students should seek further information from the recommended books and articles. This presentation is only for students and purely for academic purposes. I took/copied the pictures/maps included in the presentation are from the internet. The presenter is thankful to them and herewith courtesy is given to all. This presentation is only for academic purposes.
PHYSIOLOGY MCQS By DR. NASIR MUSTAFA (PHYSIOLOGY)



PHYSIOLOGY MCQS By DR. NASIR MUSTAFA (PHYSIOLOGY)Dr. Nasir Mustafa PHYSIOLOGY MCQS By DR. NASIR MUSTAFA (PHYSIOLOGY)
puzzle Irregular Verbs- Simple Past Tense



puzzle Irregular Verbs- Simple Past TenseOlgaLeonorTorresSnch Let´s review simple past tense, remember there are regular and irregular verbs. Here you can find some of them.
The History of Kashmir Karkota Dynasty NEP.pptx



The History of Kashmir Karkota Dynasty NEP.pptxArya Mahila P. G. College, Banaras Hindu University, Varanasi, India. This slide is an exercise for the inquisitive students preparing for the competitive examinations of the undergraduate and postgraduate students. An attempt is being made to present the slide keeping in mind the New Education Policy (NEP). An attempt has been made to give the references of the facts at the end of the slide. If new facts are discovered in the near future, this slide will be revised.
This presentation is related to the brief History of Kashmir (Part-I) with special reference to Karkota Dynasty. In the seventh century a person named Durlabhvardhan founded the Karkot dynasty in Kashmir. He was a functionary of Baladitya, the last king of the Gonanda dynasty. This dynasty ruled Kashmir before the Karkot dynasty. He was a powerful king. Huansang tells us that in his time Taxila, Singhpur, Ursha, Punch and Rajputana were parts of the Kashmir state.
Transform tomorrow: Master benefits analysis with Gen AI today webinar, 30 A...



Transform tomorrow: Master benefits analysis with Gen AI today webinar, 30 A...Association for Project Management Transform tomorrow: Master benefits analysis with Gen AI today webinar
Wednesday 30 April 2025
Joint webinar from APM AI and Data Analytics Interest Network and APM Benefits and Value Interest Network
Presenter:
Rami Deen
Content description:
We stepped into the future of benefits modelling and benefits analysis with this webinar on Generative AI (Gen AI), presented on Wednesday 30 April. Designed for all roles responsible in value creation be they benefits managers, business analysts and transformation consultants. This session revealed how Gen AI can revolutionise the way you identify, quantify, model, and realised benefits from investments.
We started by discussing the key challenges in benefits analysis, such as inaccurate identification, ineffective quantification, poor modelling, and difficulties in realisation. Learnt how Gen AI can help mitigate these challenges, ensuring more robust and effective benefits analysis.
We explored current applications and future possibilities, providing attendees with practical insights and actionable recommendations from industry experts.
This webinar provided valuable insights and practical knowledge on leveraging Gen AI to enhance benefits analysis and modelling, staying ahead in the rapidly evolving field of business transformation.
How to Create Kanban View in Odoo 18 - Odoo Slides



How to Create Kanban View in Odoo 18 - Odoo SlidesCeline George The Kanban view in Odoo is a visual interface that organizes records into cards across columns, representing different stages of a process. It is used to manage tasks, workflows, or any categorized data, allowing users to easily track progress by moving cards between stages.
Redesigning Education as a Cognitive Ecosystem: Practical Insights into Emerg...



Redesigning Education as a Cognitive Ecosystem: Practical Insights into Emerg...Leonel Morgado Slides used at the Invited Talk at the Harvard - Education University of Hong Kong - Stanford Joint Symposium, "Emerging Technologies and Future Talents", 2025-05-10, Hong Kong, China.
MCQ PHYSIOLOGY II (DR. NASIR MUSTAFA) MCQS)



MCQ PHYSIOLOGY II (DR. NASIR MUSTAFA) MCQS)Dr. Nasir Mustafa MCQ PHYSIOLOGY II (DR. NASIR MUSTAFA) MCQS)
How to Share Accounts Between Companies in Odoo 18



How to Share Accounts Between Companies in Odoo 18Celine George In this slide we’ll discuss on how to share Accounts between companies in odoo 18. Sharing accounts between companies in Odoo is a feature that can be beneficial in certain scenarios, particularly when dealing with Consolidated Financial Reporting, Shared Services, Intercompany Transactions etc.
spinal cord disorders (Myelopathies and radiculoapthies)



spinal cord disorders (Myelopathies and radiculoapthies)Mohamed Rizk Khodair Myelopathies
Radiculopathies
Myopathies (muscle disorders) for undergraduate



Myopathies (muscle disorders) for undergraduateMohamed Rizk Khodair herediatary myopthies
myotonia
inflammatory myopthies
The History of Kashmir Karkota Dynasty NEP.pptx



The History of Kashmir Karkota Dynasty NEP.pptxArya Mahila P. G. College, Banaras Hindu University, Varanasi, India.
Transform tomorrow: Master benefits analysis with Gen AI today webinar, 30 A...



Transform tomorrow: Master benefits analysis with Gen AI today webinar, 30 A...Association for Project Management
2010 PSLE Mathematics Seminar for Parents
- 1. A Seminar for Parents Helping Students withPSLE MathematicsFebruary 2010www.askyeapbanhar.blogspot.comYeap Ban HarNational Institute of EducationNanyang Technological University [email protected]
- 2. What is PSLE Mathematics?
- 3. PSLE MathematicsPaper 1 (50 min)Paper 2 (1 hr 40 min)
- 4. PSLE Foundation MathematicsPaper 1 (1 hr)Paper 2 (1 hr 15 min)
- 5. Challenging MCQsfor problems that are difficult for students to communicate solution methods
- 7. Ann, Beng and Siti each had some money at first. Ann gave Beng $0.50. Beng then gave Siti $0.75. Siti spent $0.25 on a ruler. At the end, they had $3 each. What is the difference between the amount of money that Ann and Siti had at first?$1.00$0.50$0.75$1.25Ann $3$3.50Beng $3$3.75$3.25Siti $3$3.25$2.50
- 8. What kind of curriculum is it based on?
- 10. rationale of the curriculumThe rationale of teaching mathematics is that it is “a good vehicle for the development and improvement of a person’s intellectual competence”.
- 12. Visualization – an intellectual competence - is one of the most important ability in solving problems
- 13. Basic Skillsemphasis on visualization in the learning process
- 18.
- 19. Basic Skillsmental strategies strengthen visualization ability
- 20. Find the value of 12.2 ÷ 4 .It is not expected that P6 students need to perform written working to do it.P4 students may need to perform written working as their ability in mental strategies is not as developed as that of P6 students.Basic Skills Items
- 21. 3.05312.2012.2041220 hundredths120.200.20Number Bond Method0Long Division Method
- 22. A show started at 10.55 a.m. and ended at 1.30 p.m.How long was the show in hours and minutes?It is not expected that P6 students need to perform written working to do it.P3 students may need to draw a time line as their ability in using mental strategies is not as developed as that of P6 students.Basic Skills Items
- 23. 11001330
- 24. Prawns are sold at $1.35 per 100 g at a market. What is the price of 1.5 kg of prawns? Basic Skills Items $13.50 + $6.75 = $ …Answer: $_________
- 25. Find <y in the figure below.It is not expected that P6 students need to perform written working to do it.P5 students may need to perform written working 360o – 210oas the content is new to them.Basic Skills Items70 o70 oy70 o
- 26. Basic Skillscomputation and procedures is not everything
- 27. The height of the classroom door is about __. 1 m 2 m10 m20 mSome tasks simply do not require written working.Basic Skills Items
- 28. Cup cakes are sold at 40 cents each. What is the greatest number of cup cakes that can be bought with $95? $95 ÷ 40 cents = 237.5Answer: 237 cupcakesBasic Skill Item
- 30. Basic Skillsmental computation is an important part of the curriculum
- 31. Find the value of99 + 9756 ÷ 8Find the value of200 – 53 9 x 9Find the value of73 – 15 42 ÷ 7Find the value of169 + 348 x 7
- 32. Challenging Problemswhat makes them challenging
- 33. 1 + 2 + 3 + 4 + 5 + … + 95 + 96 + 97The first 97 whole numbers are added up.What is the ones digit in the total?Challenging Items: Novel
- 34. 1 + 2 + 3 + 4 + 5 + … + 95 + 96 + 97The first 97 whole numbers are added up.What is the ones digit in the total?Challenging Items: Novel
- 35. 1 + 2 + 3 + 4 + 5 + … + 95 + 96 + 97The first 97 whole numbers are added up.What is the ones digit in the total?Challenging Items: Novel
- 36. 1 + 2 + 3 + 4 + 5 + … + 95 + 96 + 97The first 97 whole numbers are added up.What is the ones digit in the total? The method is difficult to communicate in written form. Hence, the problem is presented in the MCQ format where credit is not given for written method.Challenging Items: Novel
- 38. Table 1 consists of numbers from 1 to 56. Kay and Lin are given a plastic frame that covers exactly 9 squares of Table 1 with the centre square darkened.(a) Kay puts the frame on 9 squares as shown in the figure below.3451113192021What is the average of the 8 numbers that can be seen in the frame?
- 39. Table 1 consists of numbers from 1 to 56. Kay and Lin are given a plastic frame that covers exactly 9 squares of Table 1 with the centre square darkened.(a) Kay puts the frame on 9 squares as shown in the figure below.3+4+5+11+13+19+20 = 9696 ÷ 8 = 12345Alternate Method4 x 24 = 9696 ÷ 8 = 121113192021What is the average of the 8 numbers that can be seen in the frame?
- 40. (b) Lin puts the frame on some other 9 squares. The sum of the 8 numbers that can be seen in the frame is 272. What is the largest number that can be seen in the frame?123456789101112131415161718192021222324252627282930313233343536373839403441424344454647484950515253545556
- 41. New Emphasis on Looking for Pattern (Item from 2006) Rena used stickers of four different shapes to make a pattern. The first 12 stickers are shown below. What was the shape of the 47th sticker? ………? 1st 12th 47th
- 42. New Emphasis on Looking for Pattern (Item from 2006) Rena used stickers of four different shapes to make a pattern. The first 12 stickers are shown below. What was the shape of the 47th sticker? ………? 1 5 9
- 43. New Emphasis on Looking for Pattern (Item from 2006) Rena used stickers of four different shapes to make a pattern. The first 12 stickers are shown below. What was the shape of the 47th sticker? ………? 4 8 12
- 44. rationale of the curriculumThe rationale of teaching mathematics is that it is “a good vehicle for the development and improvement of a person’s intellectual competence”.
- 45. 9 cm26 cm2With visualization, one does not need to know a formula to calculate the area of a trapezium.
- 46. Parents Up In Arms Over PSLE Mathematics Paper TODAY’S 10 OCT 2009SINGAPORE: The first thing her son did when he came out from the Primary School Leaving Examination (PSLE) maths paper on Thursday this week was to gesture as if he was "slitting his throat". "One look at his face and I thought 'oh no'. I could see that he felt he was condemned," said Mrs Karen Sng. "When he was telling me about how he couldn't answer some of the questions, he got very emotional and started crying. He said his hopes of getting (an) A* are dashed." Not for the first time, parents are up in arms over the PSLE Mathematics paper, which some have described as "unbelievably tough" this year. As recently as two years ago, the PSLE Mathematics paper had also caused a similar uproar. The reason for Thursday's tough paper, opined the seven parents whom MediaCorp spoke to, was because Primary 6 students were allowed to use calculators while solving Paper 2 for the first time. …Said Mrs Vivian Weng: "I think the setters feel it'll be faster for them to compute with a calculator. So the problems they set are much more complex; there are more values, more steps. But it's unfair because this is the first time they can do so and they do not know what to expect!" …"The introduction of the use of calculators does not have any bearing on the difficulty of paper. The use of calculators has been introduced into the primary maths curriculum so as to enhance the teaching and learning of maths by expanding the repertoire of learning activities, to achieve a better balance between the time and effort spent developing problem solving skills and computation skills. Calculators can also help to reduce computational errors." …Another common gripe: There was not enough time for them to complete the paper. A private tutor, who declined to be named, told MediaCorp she concurred with parents' opinions. "This year's paper demanded more from students. It required them to read and understand more complex questions, and go through more steps, so time constraints would have been a concern," the 28-year-old said.
- 48. chocolatessweets12Jim121212121218Ken3 parts 12 + 12 + 12 + 12 + 18 = 661 part 22Half of the sweets Jim bought = 22 + 12 = 34So Jim bought 68 sweets.`
- 50. 180o – 2 x 21o – 2 x 28o = …
- 51. The tickets for a show are priced at $10 and $5. The number of ten-dollar tickets available is 1.5 times the number of five-dollar tickets. 5 out of 6 ten-dollar tickets and all the five-dollar tickets were sold. The ticket sales amounted to $5 600. How much more would have been collected if all the tickets were sold?FMPS
- 52. The tickets for a show are priced at $10 and $5. The number of ten-dollar tickets available is 1.5 times the number of five-dollar tickets. 5 out of 6 ten-dollar tickets and all the five-dollar tickets were sold. The ticket sales amounted to $5 600. How much more would have been collected if all the tickets were sold?FMPS7 units $5600$51 units $800$10This amount would have been collected: $5600 + $800 = $6400
- 53. Azman had 25% more marbles than Chongfu. Chongfu had 60% more marbles than Bala. During a game, Azman and Bala lost some marbles to Chongfu in the ratio 3 : 1. In the end, Azman and Bala had 780 and 480 marbles left respectively. How many marbles did Azman have at first?FMPS
- 54. Azman had 25% more marbles than Chongfu. Chongfu had 60% more marbles than Bala. During a game, Azman and Bala lost some marbles to Chongfu in the ratio 3 : 1. In the end, Azman and Bala had 780 and 480 marbles left respectively. How many marbles did Azman have at first?FMPSChongfuAzmanBala
- 55. Azman had 25% more marbles than Chongfu. Chongfu had 60% more marbles than Bala. During a game, Azman and Bala lost some marbles to Chongfu in the ratio 3 : 1. In the end, Azman and Bala had 780 and 480 marbles left respectively. How many marbles did Azman have at first?FMPS60Chongfu1006040Azman100Bala100
- 56. Azman had 25% more marbles than Chongfu. Chongfu had 60% more marbles than Bala. During a game, Azman and Bala lost some marbles to Chongfu in the ratio 3 : 1. In the end, Azman and Bala had 780 and 480 marbles left respectively. How many marbles did Azman have at first?FMPS60Chongfu100780 – 380 = 3006040Azman100Bala100
- 57. Some stamps were placed in Album A and Album B. If 30 stamps were removed from Album A, the ratio of the number of stamps in Album A to the number of stamps in Album B would be 1 : 4. If 60 stamps were removed from Album B, the ratio would be 5 : 2. How many stamps were there in Album B?FMPS








