Henry Park PSLE Seminar for Parents
Download as pptx, pdf2 likes916 views
This seminar for parents discussed the five key competencies in mathematical problem solving. Parental involvement is an important aspect of helping kids do well in school.
1 of 48
Downloaded 69 times
















































Ad
Recommended
Re sbaaa (autosaved) werfws



Re sbaaa (autosaved) werfwsAdrii Julius The document summarizes research on three important symbols in Islam: the Crescent Moon and Star, Allah, and the Kaaba. It examines the origins and meanings of each symbol, how they are represented, and their significance in Islamic beliefs and practices. Key findings include that the Crescent Moon and Star symbol predates Islam, Allah represents the one God who is the creator and judge, and the Kaaba is the holiest site in Mecca that Muslims must visit at least once in their life.
Comic Strip Vocabulary



Comic Strip VocabularyTexas A&M University San Antonio The Comic Strip Vocabulary builder invites
students to learn new words/terms by composing their own comic strips. This method intends to create vivid mental images and visual word association for the reader.
CSEC Physics PD Lab - Factors affecting strength of electromagnet



CSEC Physics PD Lab - Factors affecting strength of electromagnetRonaldo Degazon Hypothesis: The 4 factors which can affect the strength of an electromagnet are the type of core used, the number of turns of wire, the magnitude of the current used and the shape of the solenoid.
Aim: To investigate the factors which affect the strength of an electromagnet.
CSEC Results - Territorial Merit List 2014 - Jamaica



CSEC Results - Territorial Merit List 2014 - JamaicaRushane Barnes This document lists the top performing candidates in various CSEC subjects for Jamaica in June 2014. It provides the rank, candidate number, name, school, and grades for the top candidates in subjects like Agricultural Science, Biology, Caribbean History, Chemistry, Clothing and Textiles, Economics, English A, English B, Food and Nutrition, and French. The top students achieved grades of A or A grades with distinction in the various subjects.
CAPE® 2021 Merit List by Subject from Caribbean Examinations Council



CAPE® 2021 Merit List by Subject from Caribbean Examinations CouncilCaribbean Examinations Council The document lists the top performing candidates from the Caribbean region in various CAPE subjects in the June 2021 examinations. It provides the names, schools, grades and countries of the top 10 candidates in subjects like Accounting, Agricultural Science, Applied Mathematics, Art and Design, Biology, Chemistry and others. The top candidate for Communication Studies was Angelina Jaya Siew from Naparima Girls' High School in Trinidad and Tobago.
Social studies sba about domestic violence



Social studies sba about domestic violenceSamuel Beckford this sba is about domestic violence you can view and download it for further usage my recommendation needs to be fixed i don't think it's accurate.
English proficiency test 2017



English proficiency test 2017Jenica Torres This document contains a reading comprehension subset that aims to test the ability to recognize standard written English. It consists of 15 incomplete sentences with 4 response options each. The sentences cover a variety of topics and test grammar, such as verb tense and subject-verb agreement. The goal is to choose the response that best completes each sentence.
How to make book trailers



How to make book trailersivanhoejenny This document provides step-by-step instructions for creating a book trailer in 5 steps: 1) Identify important plot points, 2) Collect relevant images, 3) Find background music, 4) Add sound effects, and 5) Assemble the trailer using video editing software. It also includes links to free resources for images, music, sound effects and video tutorials for creating book trailers in programs like Movie Maker and PowerPoint. The goal is to hook viewers and get them interested in reading the book through a combination of visuals, audio and brevity.
How to Ace PSLE Maths



How to Ace PSLE MathsJimmy Keng The document provides information about preparing for and taking the PSLE Mathematics exam in Singapore. It discusses the structure of the exam, which consists of two papers, and outlines the curriculum focus on problem solving. It also provides examples of different types of math problems students may encounter on the exam. At the end, it discusses a news article where parents complained that this year's PSLE math exam was unusually difficult, possibly because it was the first year calculators were allowed.
Bendermeer Primary School Seminar for Parents



Bendermeer Primary School Seminar for ParentsJimmy Keng This document provides an overview of a presentation on helping children with primary mathematics. It discusses how mathematics can develop intellectual competence and reflects on shifts in test questions to require more conceptual understanding and real-world problem solving over rote algorithms. Examples of math questions and lessons from various primary grades in Singapore, the US, UK, Netherlands and Japan are presented, covering topics like number sense, patterns, problem solving and visual models. Key competencies and strategies for problem solving are discussed.
PSLE 2011 - (Number x Value)



PSLE 2011 - (Number x Value)sunnytkk The document is a math word problem about how many 80-cent stamps Jane can buy if she spent a total of $30.60 and bought twice as many 50-cent stamps as 80-cent stamps. It shows the steps of setting up an equation relating the number of each stamp multiplied by its price equals the total amount spent, and then solving the equation to determine Jane can buy 17 80-cent stamps.
Seminar for Parents on PSLE Mathematics



Seminar for Parents on PSLE MathematicsJimmy Keng This document provides information about coaching children in primary mathematics for the PSLE:
1) It discusses 3 things about problem solving in the PSLE and 2 sections that assess challenging problem solving.
2) It outlines a 5-step process to help children with challenging problems and provides 2 examples demonstrating the steps.
3) Marshall Cavendish Institute is offering a 4-session workshop for parents/tutors to understand the primary math curriculum and coach topics like fractions, geometry, word problems, and algebra.
2010 PSLE Mathematics Seminar for Parents



2010 PSLE Mathematics Seminar for ParentsJimmy Keng Seminar for Parents
Fairfield Methodist Primary School & Griffiths Primary School
26 & 27 February 2010
Parents Seminar on Heuristics at Chongfu School



Parents Seminar on Heuristics at Chongfu SchoolJimmy Keng This is the set of slides used at the seminar for Primary Five parents at Chongfu School in March 2011.
Maths Hub June 2015 Day 1 and Day 2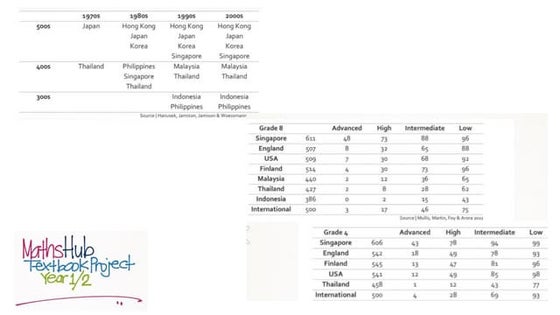



Maths Hub June 2015 Day 1 and Day 2Jimmy Keng This document discusses differentiating instruction to challenge advanced learners. It provides examples of ways to assess basic subtraction skills through runway indicators. For advanced learners, it suggests having them solve problems in alternative ways, write stories for equations, or write notes applying math concepts to enrich their learning beyond basic skills.
32 teaching strategies in math 



32 teaching strategies in math Cordova Public College and University of Cebu-LapuLapu-Mandaue This document discusses several teaching strategies for math: Lecture-Discussion Method, Cooperative and Collaborative Learning, Jigsaw Method, and Think-Pair-Share. It provides details on how each strategy works, including applying the Lecture-Discussion Method with its nine events of instruction, the emphasis of cooperative/collaborative learning, and examples of applying the Jigsaw Method and Think-Pair-Share in a classroom.
Lower Primary Maths Problem Solving



Lower Primary Maths Problem SolvingJimmy Keng The document discusses various problem solving heuristics for lower primary mathematics. It provides 14 examples of word problems demonstrating different heuristics students can use to solve problems, such as using tables, looking for patterns, guess and check, and breaking problems into steps. The heuristics allow students to systematically solve problems even if they are initially unfamiliar.
Approaches in teaching and learning mathematics



Approaches in teaching and learning mathematicstangyokechoo The document discusses several approaches to teaching and learning mathematics:
1. Cooperative learning involves students working together in groups, under teacher supervision, to solve problems and complete projects while the teacher evaluates learning outcomes.
2. Contextual learning relates new knowledge to students' life experiences and environments to make learning more meaningful.
3. Mastery learning breaks the curriculum into small units to ensure students master one unit before moving to the next, with remedial activities as needed.
4. Constructivism and self-access learning encourage students to build knowledge based on their own exploration and prior experiences with teacher guidance.
5. Future studies prepares students to be independent thinkers by understanding future issues and acquiring lifelong learning skills.
Strategies in teaching mathematics



Strategies in teaching mathematicsMaria Veronica Lee Makayan The document provides strategies for teaching mathematics. It discusses strategies based on knowledge and skill goals as well as understanding goals. For knowledge and skill goals, repetition and practice are emphasized. For understanding goals, teacher-led discussion and discovery-based laboratory activities are recommended. Problem solving strategies include ensuring student understanding, asking questions, encouraging reflection on solutions, and presenting alternative problem solving approaches. Constructivist learning and cognitive tools like guided discovery are also discussed. The document outlines steps for problem solving and strategies like concept attainment. It concludes by evaluating mathematics learning through various individual and group tests as well as informal and standardized testing procedures.
Techniques and Strategies in Teaching Math



Techniques and Strategies in Teaching MathAlyssa Marie Bautista The document discusses strategies for teaching mathematics, including discovery approach, inquiry teaching, demonstration approach, math-lab approach, practical work approach, individualized instruction using modules, brainstorming, problem-solving, cooperative learning, and integrative technique. It provides details on each approach, such as the discovery approach aiming to develop higher-order thinking skills and both teachers and learners playing active roles. It also lists 10 creative ways to teach math using dramatizations, children's bodies, play, toys, stories, creativity, and problem-solving abilities.
AME PSLE Seminar



AME PSLE SeminarJimmy Keng PSLE Mathematics Seminar
Association of Mathematics Educators
Dr. Yeap Ban Har
National Institute of Education
Nanyang Technological University
This seminar was conducted at Singapore Polytechnic.
Parents Seminar on PSLE Mathematics



Parents Seminar on PSLE MathematicsJimmy Keng Here are some tips for improving problem solving skills in PSLE Mathematics:
- Take time to understand the question fully before attempting to solve it. Re-read if needed.
- Look for key information like numbers, operations, shapes etc and think about how they might be related.
- Draw diagrams or make lists when working with multiple steps, relationships or parts. This helps organize your thinking.
- Estimate answers before calculating to check if your working makes sense.
- Check your work - go back and ensure steps are correct and you have not made computational errors.
- Practice explaining your reasoning and showing your working, as this helps develop logical thinking skills.
- Review incorrect or challenging questions again later
Boston College, Mathematics Education Seminar Series by Yeap Ban Har 14 April...



Boston College, Mathematics Education Seminar Series by Yeap Ban Har 14 April...Jimmy Keng The document discusses several key aspects of mathematics education in Singapore schools that have contributed to high student achievement, including an emphasis on curriculum development, teacher training, assessment, and societal expectations. It provides insights into Singapore's education system structure from primary to post-secondary levels, curriculum focus on problem solving, emphasis on concrete to abstract learning, and presence of intervention programs to support students at different levels.
Paradigms In Mathematical Education For The 21st Century 22 24 October 2009 V...



Paradigms In Mathematical Education For The 21st Century 22 24 October 2009 V...Jimmy Keng TEACHING & LEARNING OF MATHEMATICS IN SINGAPORE
Yeap Ban Har
National Institute of Education
Nanyang Technological University
Singapore
International School Saigon Pearl



International School Saigon PearlJimmy Keng This document summarizes a seminar on the Singapore Math approach. It discusses key concepts like conceptual understanding, variation theory, concrete-pictorial-abstract instruction, and assessment results that show Singapore student performance. Example word problems are provided to illustrate how Singapore Math teaches for understanding over rote memorization.
Catholic Education Council Seminar Jakarta Mpk 22 Jan



Catholic Education Council Seminar Jakarta Mpk 22 JanJimmy Keng Mentari - Catholic Education Council (MPK) Seminar
January 2010
Teaching Mathematics in Effectively for the 21st Century
Helping Students with PSLE Mathematics_6 February 2010



Helping Students with PSLE Mathematics_6 February 2010Jimmy Keng The document summarizes key points from a seminar for parents and tutors on helping students with Primary School Leaving Examination (PSLE) mathematics. It discusses the format and content of the PSLE math papers, including the introduction of calculators for Paper 2. It also reports on parents being upset over the perceived difficulty of this year's PSLE math paper due to more complex questions involving more steps and values as a result of allowing calculator use.
Helping Students with PSLE Mathematics_6 February 2010



Helping Students with PSLE Mathematics_6 February 2010Jimmy Keng A Seminar for Parents & Tutors
Helping Students with
PSLE Mathematics
6 February 2010
SINGAPOTE TEACHERS’ UNION
Yeap Ban Har
National Institute of Education
Nanyang Technological University
Singapore
Ad
More Related Content
Viewers also liked (14)
How to Ace PSLE Maths



How to Ace PSLE MathsJimmy Keng The document provides information about preparing for and taking the PSLE Mathematics exam in Singapore. It discusses the structure of the exam, which consists of two papers, and outlines the curriculum focus on problem solving. It also provides examples of different types of math problems students may encounter on the exam. At the end, it discusses a news article where parents complained that this year's PSLE math exam was unusually difficult, possibly because it was the first year calculators were allowed.
Bendermeer Primary School Seminar for Parents



Bendermeer Primary School Seminar for ParentsJimmy Keng This document provides an overview of a presentation on helping children with primary mathematics. It discusses how mathematics can develop intellectual competence and reflects on shifts in test questions to require more conceptual understanding and real-world problem solving over rote algorithms. Examples of math questions and lessons from various primary grades in Singapore, the US, UK, Netherlands and Japan are presented, covering topics like number sense, patterns, problem solving and visual models. Key competencies and strategies for problem solving are discussed.
PSLE 2011 - (Number x Value)



PSLE 2011 - (Number x Value)sunnytkk The document is a math word problem about how many 80-cent stamps Jane can buy if she spent a total of $30.60 and bought twice as many 50-cent stamps as 80-cent stamps. It shows the steps of setting up an equation relating the number of each stamp multiplied by its price equals the total amount spent, and then solving the equation to determine Jane can buy 17 80-cent stamps.
Seminar for Parents on PSLE Mathematics



Seminar for Parents on PSLE MathematicsJimmy Keng This document provides information about coaching children in primary mathematics for the PSLE:
1) It discusses 3 things about problem solving in the PSLE and 2 sections that assess challenging problem solving.
2) It outlines a 5-step process to help children with challenging problems and provides 2 examples demonstrating the steps.
3) Marshall Cavendish Institute is offering a 4-session workshop for parents/tutors to understand the primary math curriculum and coach topics like fractions, geometry, word problems, and algebra.
2010 PSLE Mathematics Seminar for Parents



2010 PSLE Mathematics Seminar for ParentsJimmy Keng Seminar for Parents
Fairfield Methodist Primary School & Griffiths Primary School
26 & 27 February 2010
Parents Seminar on Heuristics at Chongfu School



Parents Seminar on Heuristics at Chongfu SchoolJimmy Keng This is the set of slides used at the seminar for Primary Five parents at Chongfu School in March 2011.
Maths Hub June 2015 Day 1 and Day 2



Maths Hub June 2015 Day 1 and Day 2Jimmy Keng This document discusses differentiating instruction to challenge advanced learners. It provides examples of ways to assess basic subtraction skills through runway indicators. For advanced learners, it suggests having them solve problems in alternative ways, write stories for equations, or write notes applying math concepts to enrich their learning beyond basic skills.
32 teaching strategies in math 



32 teaching strategies in math Cordova Public College and University of Cebu-LapuLapu-Mandaue This document discusses several teaching strategies for math: Lecture-Discussion Method, Cooperative and Collaborative Learning, Jigsaw Method, and Think-Pair-Share. It provides details on how each strategy works, including applying the Lecture-Discussion Method with its nine events of instruction, the emphasis of cooperative/collaborative learning, and examples of applying the Jigsaw Method and Think-Pair-Share in a classroom.
Lower Primary Maths Problem Solving



Lower Primary Maths Problem SolvingJimmy Keng The document discusses various problem solving heuristics for lower primary mathematics. It provides 14 examples of word problems demonstrating different heuristics students can use to solve problems, such as using tables, looking for patterns, guess and check, and breaking problems into steps. The heuristics allow students to systematically solve problems even if they are initially unfamiliar.
Approaches in teaching and learning mathematics



Approaches in teaching and learning mathematicstangyokechoo The document discusses several approaches to teaching and learning mathematics:
1. Cooperative learning involves students working together in groups, under teacher supervision, to solve problems and complete projects while the teacher evaluates learning outcomes.
2. Contextual learning relates new knowledge to students' life experiences and environments to make learning more meaningful.
3. Mastery learning breaks the curriculum into small units to ensure students master one unit before moving to the next, with remedial activities as needed.
4. Constructivism and self-access learning encourage students to build knowledge based on their own exploration and prior experiences with teacher guidance.
5. Future studies prepares students to be independent thinkers by understanding future issues and acquiring lifelong learning skills.
Strategies in teaching mathematics



Strategies in teaching mathematicsMaria Veronica Lee Makayan The document provides strategies for teaching mathematics. It discusses strategies based on knowledge and skill goals as well as understanding goals. For knowledge and skill goals, repetition and practice are emphasized. For understanding goals, teacher-led discussion and discovery-based laboratory activities are recommended. Problem solving strategies include ensuring student understanding, asking questions, encouraging reflection on solutions, and presenting alternative problem solving approaches. Constructivist learning and cognitive tools like guided discovery are also discussed. The document outlines steps for problem solving and strategies like concept attainment. It concludes by evaluating mathematics learning through various individual and group tests as well as informal and standardized testing procedures.
Techniques and Strategies in Teaching Math



Techniques and Strategies in Teaching MathAlyssa Marie Bautista The document discusses strategies for teaching mathematics, including discovery approach, inquiry teaching, demonstration approach, math-lab approach, practical work approach, individualized instruction using modules, brainstorming, problem-solving, cooperative learning, and integrative technique. It provides details on each approach, such as the discovery approach aiming to develop higher-order thinking skills and both teachers and learners playing active roles. It also lists 10 creative ways to teach math using dramatizations, children's bodies, play, toys, stories, creativity, and problem-solving abilities.
Similar to Henry Park PSLE Seminar for Parents (20)
AME PSLE Seminar



AME PSLE SeminarJimmy Keng PSLE Mathematics Seminar
Association of Mathematics Educators
Dr. Yeap Ban Har
National Institute of Education
Nanyang Technological University
This seminar was conducted at Singapore Polytechnic.
Parents Seminar on PSLE Mathematics



Parents Seminar on PSLE MathematicsJimmy Keng Here are some tips for improving problem solving skills in PSLE Mathematics:
- Take time to understand the question fully before attempting to solve it. Re-read if needed.
- Look for key information like numbers, operations, shapes etc and think about how they might be related.
- Draw diagrams or make lists when working with multiple steps, relationships or parts. This helps organize your thinking.
- Estimate answers before calculating to check if your working makes sense.
- Check your work - go back and ensure steps are correct and you have not made computational errors.
- Practice explaining your reasoning and showing your working, as this helps develop logical thinking skills.
- Review incorrect or challenging questions again later
Boston College, Mathematics Education Seminar Series by Yeap Ban Har 14 April...



Boston College, Mathematics Education Seminar Series by Yeap Ban Har 14 April...Jimmy Keng The document discusses several key aspects of mathematics education in Singapore schools that have contributed to high student achievement, including an emphasis on curriculum development, teacher training, assessment, and societal expectations. It provides insights into Singapore's education system structure from primary to post-secondary levels, curriculum focus on problem solving, emphasis on concrete to abstract learning, and presence of intervention programs to support students at different levels.
Paradigms In Mathematical Education For The 21st Century 22 24 October 2009 V...



Paradigms In Mathematical Education For The 21st Century 22 24 October 2009 V...Jimmy Keng TEACHING & LEARNING OF MATHEMATICS IN SINGAPORE
Yeap Ban Har
National Institute of Education
Nanyang Technological University
Singapore
International School Saigon Pearl



International School Saigon PearlJimmy Keng This document summarizes a seminar on the Singapore Math approach. It discusses key concepts like conceptual understanding, variation theory, concrete-pictorial-abstract instruction, and assessment results that show Singapore student performance. Example word problems are provided to illustrate how Singapore Math teaches for understanding over rote memorization.
Catholic Education Council Seminar Jakarta Mpk 22 Jan



Catholic Education Council Seminar Jakarta Mpk 22 JanJimmy Keng Mentari - Catholic Education Council (MPK) Seminar
January 2010
Teaching Mathematics in Effectively for the 21st Century
Helping Students with PSLE Mathematics_6 February 2010



Helping Students with PSLE Mathematics_6 February 2010Jimmy Keng The document summarizes key points from a seminar for parents and tutors on helping students with Primary School Leaving Examination (PSLE) mathematics. It discusses the format and content of the PSLE math papers, including the introduction of calculators for Paper 2. It also reports on parents being upset over the perceived difficulty of this year's PSLE math paper due to more complex questions involving more steps and values as a result of allowing calculator use.
Helping Students with PSLE Mathematics_6 February 2010



Helping Students with PSLE Mathematics_6 February 2010Jimmy Keng A Seminar for Parents & Tutors
Helping Students with
PSLE Mathematics
6 February 2010
SINGAPOTE TEACHERS’ UNION
Yeap Ban Har
National Institute of Education
Nanyang Technological University
Singapore
Chile MOE Seminar English



Chile MOE Seminar EnglishJimmy Keng This is the English version of the presentation at Avancemos en las Matematicas: La Mirada de Singapur
Mohd Izham



Mohd Izham376673 The document discusses methods to enhance pupils' interest in a special remedial class. Three activities are implemented: 1) A grading system to motivate pupils, 2) Using worksheets with cartoon characters, and 3) A board game combining reading, math, and movement. Observations found these methods increased task completion, attention, and test scores. The goal of improving interest to aid learning was achieved by incorporating elements pupils found engaging. Close supervision is needed to ensure activities are implemented effectively.
Weston Public Schools 2012



Weston Public Schools 2012Jimmy Keng These were the materials covered in last year's professional development. This year's session is a follow-up with revisiting of core ideas and extension of others.
ARK Schools, London 



ARK Schools, London Jimmy Keng This is a one-day course on Essentials of Singapore Maths which is equivalent to MAP101 Fundamentals of Singapore Mathematics. About 60 participants attended this session.
AMSTI Event, Birmingham, Alabama



AMSTI Event, Birmingham, AlabamaJimmy Keng This document summarizes Singapore's approach to mathematics education. It discusses how Singapore Math emphasizes conceptual understanding through concrete experiences and visual representations. It highlights Singapore's high performance on international assessments like TIMSS and PISA. It also outlines recent developments in Singapore's mathematics curriculum, pedagogy, textbooks, and use of technology and learning support strategies to help all students succeed.
Minilessons for math_practice_g3-5



Minilessons for math_practice_g3-5Dania493634 This document provides an overview of the book "Minilessons for Math Practice, Grades 3–5" by Rusty Bresser and Caren Holtzman. The book presents 27 quick math activities that take 5-15 minutes and require little preparation. The activities are designed to provide practice for upper elementary students on key math concepts like number operations, algebra, geometry, data analysis, and measurement. Each activity includes instructions, questions for students, an example classroom scenario, and extension ideas. The goal is to broaden what it means to provide math practice and enhance students' understanding through applying skills in various problem-solving contexts throughout the school day.
Accomplishment report math



Accomplishment report mathReon Zedval This document provides an accomplishment report on mathematics teaching from Calapan Elementary School in Tarlac Province, Philippines for the 2013-2014 school year. It summarizes the activities undertaken by mathematics teachers such as preparing quarterly tests, conducting reviews, and participating in math competitions. It provides the achievement rates and test results for each grade level on the national and quarterly assessments. Issues encountered and recommendations for addressing them are also discussed. Pictorial examples of teaching tools used are listed at the end.
Math teaching approaches that work



Math teaching approaches that workSargodhains' Institute for Professional Development The presnetation will highlight ways of effective mathematics teaching and how a teacher can adapt it.
St Edward's School, Florida



St Edward's School, FloridaJimmy Keng This was from the professional development course for lower school teachers at a school in Vero Beach, Florida.
NCTM 2010 Regional Conferences & Expositions Denver 2



NCTM 2010 Regional Conferences & Expositions Denver 2Jimmy Keng This session focuses on eight elements of early grade mathematics in Singapore that help develop a strong foundation for later mathematics learning. These include: 1) Sustained focus on thinking, 2) Focusing on a small number of topics taught in-depth, 3) Using concrete-pictorial-abstract approaches, 4) Having a spiral curriculum where topics are revisited over multiple years, 5) Utilizing non-specialist teachers with support materials, 6) Systematically varying tasks, 7) High aspirations among parents, and 8) Providing learning support and remediation. Concrete approaches, visual representations, and attention to disadvantaged students helps ensure all students learn well.
Seminar at Harvard Graduate School of Education 15 April 2010



Seminar at Harvard Graduate School of Education 15 April 2010Jimmy Keng The document discusses several theories that underpin the approach to mathematics education in Singapore. It discusses Bruner's theory of moving from concrete to pictorial to abstract representations. It also discusses Skemp's theory of relational versus instrumental understanding. Dienes' theory of variation to aid conceptual understanding is also summarized. Examples are provided of how these theories are implemented in Singapore math textbooks and lessons through concrete models, pictorial representations, and variations in problems.
Singapore math @ sheraton



Singapore math @ sheratonguest009ebb The document discusses the theoretical underpinnings of the Singapore Math approach. It describes three key theories that influenced the development of Singapore Math:
1. Bruner's theory of the concrete-pictorial-abstract approach to help students develop a strong mathematical foundation.
2. Skemp's theory of conceptual understanding versus procedural understanding, with Singapore Math emphasizing the former.
3. Dienes' theory of variation in mathematics education through perceptual and mathematical variability in tasks.
The document provides examples of how these theories are applied in Singapore Math teaching materials, lessons, and instructional models.
Ad
More from Jimmy Keng (20)
Math Plus Kansas City



Math Plus Kansas CityJimmy Keng The document discusses using math journals in elementary school classrooms to teach mathematical concepts. It describes a framework for teaching mastery that involves anchor tasks, guided practice, and independent practice. Journaling is presented as one part of this process where students explore concepts, structure their understanding, and reflect on their learning. Examples are provided of kindergarteners recording number bonds in their journals to master basic counting and addition. The journal entries allow teachers to assess understanding and provide differentiated instruction.
Primary Mathematics Fractions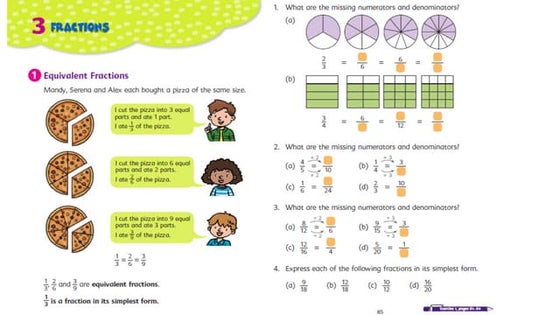



Primary Mathematics FractionsJimmy Keng Basic Lesson Structure of Singapore Math - anchor task, guided practice and independent practice
Blake School Presentation Grade 1



Blake School Presentation Grade 1Jimmy Keng The document outlines a schedule for four sessions occurring between 08:30-04:00 with a forum period from 03:30-04:00. It then discusses using a lesson on the Common Core to understand critical areas for Grade 1, including number bonds, comparison of numbers, and conservation of numbers. Various methods for developing visualization like the CPA approach, bar models, and teacher questioning are listed. The document goes on to discuss elements of effective math lessons including exploration, structure, journaling, reflection, and guided/independent practice using addition and subtraction strategies like counting all, making 10, subtracting from ten, and renaming before subtracting with examples provided.
Blake Grade 6



Blake Grade 6Jimmy Keng This document provides an overview of a middle school mathematics institute that will take place on Saturday. It discusses the basic lesson format, which includes an anchor task, guided practice, and independent practice. It also references Bruner's idea of using concrete experiences and pictorial representations to help students understand abstract ideas. The document then provides several case studies as examples of lessons that could be used to develop, apply, and practice various mathematical concepts involving fractions, algebra, geometry, and more.
Blake grade 5



Blake grade 5Jimmy Keng This document provides an overview of a Grade 5 mathematics institute that will take place on a Friday. It outlines the basic lesson format, which includes an anchor task, guided practice, and independent practice. It also references several learning theories that provide a framework for the lesson, such as Bruner's idea of concrete, iconic, and symbolic representations. The document includes several math word problems from past PSLE exams in Singapore to use for practice. It concludes with key learning theories covered and strategies for challenging advanced learners.
Blake Grade 4



Blake Grade 4Jimmy Keng 1) The document discusses standards and instructional focus areas for Grade 4 mathematics, including multi-digit multiplication and division, fractions, and geometric shapes.
2) It provides examples of case studies to solve, including arranging fractions in order and word problems involving fractions of amounts.
3) Theories of learning and representation discussed include Bruner's CPA approach and Skemp's classifications of understanding in mathematics.
Blake Grade 3



Blake Grade 3Jimmy Keng This document provides information about a grade 3 mathematics institute to be held on Wednesday. It discusses key theories in mathematics learning from Piaget, Bruner, Dienes, Vygotsky, and Skemp. The document also provides several case studies with examples of lesson plans and problems that assess different mathematical concepts like operations, fractions, problem solving, and place value.
Blake Grade 2



Blake Grade 2Jimmy Keng The document discusses a Grade 2 math institute that will focus on place value using concrete and pictorial representations. It provides several case studies on topics like subtraction across zeros, fractions, and problem solving. The lessons follow a basic format of an anchor task, guided practice, and independent practice. Key learning theories that will be drawn from include those from Piaget, Bruner, Dienes, Vygotsky, and Skemp. Bruner's CPA approach and Skemp's classifications of understanding will be particularly relevant for using different representations to build conceptual and relational understanding.
Blake Grade 1



Blake Grade 1Jimmy Keng Participants to Blake School Singapore Math Institute in June 2015 please download and print this set of handouts.
2104 WSU Cutouts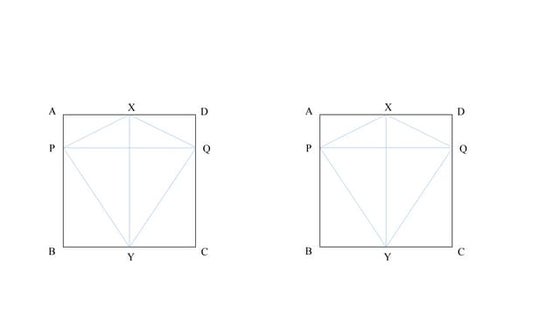



2104 WSU CutoutsJimmy Keng This document contains instructions for cutting out numbers and mathematical symbols from a page. It includes numbers from 0 to 9, basic mathematical operators like + and -, and instructions to cut out the listed items. The document is repetitive, listing the same numbers and symbols twice.
2014 WSU Handouts



2014 WSU HandoutsJimmy Keng The document summarizes discussions from breakout sessions at the 4th Singapore Math Institute on teaching mathematics using Singapore's approach. It provides tasks and problems from Singapore classrooms related to practicing skills through problem-solving, using anchor tasks to structure lessons, and teaching geometry in grades 4-6. The goals are to emulate Singapore's emphasis on problem-solving and multi-step word problems to develop students' mathematical thinking.
2014 WSU Day 2



2014 WSU Day 2Jimmy Keng The document discusses strategies for developing and improving mathematical practices, such as using anchor tasks, collaborative structures, questioning techniques, journals, textbooks for reflection, and focusing on visualization, generalization, and number sense. It also discusses moving from concrete to pictorial to abstract representations, and using anchor tasks and challenging word problems to teach Singapore math concepts.
2014 WSU Day 1 Slides



2014 WSU Day 1 SlidesJimmy Keng This document discusses using a problem-solving approach to teach mathematics. It focuses on practicing problem-solving lessons and breaking students into groups to work on problems. The document provides resources for lesson plans and contact information for the speaker who advocates for integrating problem-solving into mathematics education.
Se01 abc's of singapore math through whole numbers



Se01 abc's of singapore math through whole numbersJimmy Keng The document discusses the Singapore approach to teaching mathematics, which was developed to help Singaporean students perform better in math. It is based on Bruner's ideas of a spiral curriculum and using representations. The document provides 15 sample math tasks that demonstrate fundamentals of Singapore Math instruction, such as the Concrete-Pictorial-Abstract approach. It also includes quotes from Bruner about revisiting basic ideas repeatedly to help students master structured bodies of knowledge.
Sd09 visualization



Sd09 visualizationJimmy Keng This document contains an agenda for a staff development conference on Singapore Math strategies with a focus on visualization. It includes 4 sample math tasks: 1) finding the area of a 4-sided polygon on a geoboard; 2) calculating leftover wire used to make a figure of 6 equilateral triangles; 3) dividing numbers by 3, 4, and 6; and 4) a word problem about Peter and Nancy exchanging coins to determine how many Peter originally had. The tasks are meant to illustrate ways to get students to visualize math concepts.
Sd02 challenge me



Sd02 challenge meJimmy Keng The document discusses strategies for differentiated instruction for advanced learners. It focuses on enrichment rather than acceleration. It provides 6 case studies as examples of anchor tasks that can challenge advanced learners in lessons, including problems about number sequences, geometry of rooms and chairs, properties of triangles, and finding sums of hexagon angles. The goal of the session is to explore general strategies for differentiating instruction to meet the needs of advanced students.
Ad
Recently uploaded (20)
PHYSIOLOGY MCQS By DR. NASIR MUSTAFA (PHYSIOLOGY)



PHYSIOLOGY MCQS By DR. NASIR MUSTAFA (PHYSIOLOGY)Dr. Nasir Mustafa PHYSIOLOGY MCQS By DR. NASIR MUSTAFA (PHYSIOLOGY)
The History of Kashmir Karkota Dynasty NEP.pptx



The History of Kashmir Karkota Dynasty NEP.pptxArya Mahila P. G. College, Banaras Hindu University, Varanasi, India. This slide is an exercise for the inquisitive students preparing for the competitive examinations of the undergraduate and postgraduate students. An attempt is being made to present the slide keeping in mind the New Education Policy (NEP). An attempt has been made to give the references of the facts at the end of the slide. If new facts are discovered in the near future, this slide will be revised.
This presentation is related to the brief History of Kashmir (Part-I) with special reference to Karkota Dynasty. In the seventh century a person named Durlabhvardhan founded the Karkot dynasty in Kashmir. He was a functionary of Baladitya, the last king of the Gonanda dynasty. This dynasty ruled Kashmir before the Karkot dynasty. He was a powerful king. Huansang tells us that in his time Taxila, Singhpur, Ursha, Punch and Rajputana were parts of the Kashmir state.
Cultivation Practice of Turmeric in Nepal.pptx



Cultivation Practice of Turmeric in Nepal.pptxUmeshTimilsina1 Cultivation Practice of Turmeric in Nepal
2025 The Senior Landscape and SET plan preparations.pptx



2025 The Senior Landscape and SET plan preparations.pptxmansk2 2025 The Senior Landscape and SET plan preparations.pptx
How to Manage Upselling in Odoo 18 Sales



How to Manage Upselling in Odoo 18 SalesCeline George In this slide, we’ll discuss on how to manage upselling in Odoo 18 Sales module. Upselling in Odoo is a powerful sales technique that allows you to increase the average order value by suggesting additional or more premium products or services to your customers.
ANTI-VIRAL DRUGS unit 3 Pharmacology 3.pptx



ANTI-VIRAL DRUGS unit 3 Pharmacology 3.pptxMayuri Chavan ANTI-VIRAL DRUGS unit 3 Pharmacology 3.pptx
E-Filing_of_Income_Tax.pptx and concept of form 26AS



E-Filing_of_Income_Tax.pptx and concept of form 26ASAbinash Palangdar Now everyone needs to file return electronically. This ppt will help to to file return.
Ancient Stone Sculptures of India: As a Source of Indian History



Ancient Stone Sculptures of India: As a Source of Indian HistoryVirag Sontakke This Presentation is prepared for Graduate Students. A presentation that provides basic information about the topic. Students should seek further information from the recommended books and articles. This presentation is only for students and purely for academic purposes. I took/copied the pictures/maps included in the presentation are from the internet. The presenter is thankful to them and herewith courtesy is given to all. This presentation is only for academic purposes.
Bridging the Transit Gap: Equity Drive Feeder Bus Design for Southeast Brooklyn



Bridging the Transit Gap: Equity Drive Feeder Bus Design for Southeast Brooklyni4jd41bk Group presentation of a feasibility and cost benefit study for a proposed bus service in Southeastern Brooklyn, New York.
Rock Art As a Source of Ancient Indian History



Rock Art As a Source of Ancient Indian HistoryVirag Sontakke This Presentation is prepared for Graduate Students. A presentation that provides basic information about the topic. Students should seek further information from the recommended books and articles. This presentation is only for students and purely for academic purposes. I took/copied the pictures/maps included in the presentation are from the internet. The presenter is thankful to them and herewith courtesy is given to all. This presentation is only for academic purposes.
Overview Well-Being and Creative Careers



Overview Well-Being and Creative CareersUniversity of Amsterdam Slides to support presentations and the publication of my book Well-Being and Creative Careers: What Makes You Happy Can Also Make You Sick, out in September 2025 with Intellect Books in the UK and worldwide, distributed in the US by The University of Chicago Press.
In this book and presentation, I investigate the systemic issues that make creative work both exhilarating and unsustainable. Drawing on extensive research and in-depth interviews with media professionals, the hidden downsides of doing what you love get documented, analyzing how workplace structures, high workloads, and perceived injustices contribute to mental and physical distress.
All of this is not just about what’s broken; it’s about what can be done. The talk concludes with providing a roadmap for rethinking the culture of creative industries and offers strategies for balancing passion with sustainability.
With this book and presentation I hope to challenge us to imagine a healthier future for the labor of love that a creative career is.
CNS infections (encephalitis, meningitis & Brain abscess



CNS infections (encephalitis, meningitis & Brain abscessMohamed Rizk Khodair CNS infections (encephalitis, meningitis & Brain abscess)
Myopathies (muscle disorders) for undergraduate



Myopathies (muscle disorders) for undergraduateMohamed Rizk Khodair herediatary myopthies
myotonia
inflammatory myopthies
BÀI TẬP BỔ TRỢ TIẾNG ANH 9 THEO ĐƠN VỊ BÀI HỌC - GLOBAL SUCCESS - CẢ NĂM (TỪ...



BÀI TẬP BỔ TRỢ TIẾNG ANH 9 THEO ĐƠN VỊ BÀI HỌC - GLOBAL SUCCESS - CẢ NĂM (TỪ...Nguyen Thanh Tu Collection https://app.box.com/s/yfwqwcillls0z4p34958pr8nj0b4udyr
antiquity of writing in ancient India- literary & archaeological evidence



antiquity of writing in ancient India- literary & archaeological evidencePrachiSontakke5 for the students of BA Sem
All About the 990 Unlocking Its Mysteries and Its Power.pdf



All About the 990 Unlocking Its Mysteries and Its Power.pdfTechSoup In this webinar, nonprofit CPA Gregg S. Bossen shares some of the mysteries of the 990, IRS requirements — which form to file (990N, 990EZ, 990PF, or 990), and what it says about your organization, and how to leverage it to make your organization shine.
The History of Kashmir Karkota Dynasty NEP.pptx



The History of Kashmir Karkota Dynasty NEP.pptxArya Mahila P. G. College, Banaras Hindu University, Varanasi, India.
BÀI TẬP BỔ TRỢ TIẾNG ANH 9 THEO ĐƠN VỊ BÀI HỌC - GLOBAL SUCCESS - CẢ NĂM (TỪ...



BÀI TẬP BỔ TRỢ TIẾNG ANH 9 THEO ĐƠN VỊ BÀI HỌC - GLOBAL SUCCESS - CẢ NĂM (TỪ...Nguyen Thanh Tu Collection
Henry Park PSLE Seminar for Parents
- 1. PSLE Mathematics Seminar for ParentsHenry Park Primary SchoolOrganised by Henry Park Alumni AssociationMay 2010Yeap Ban HarNational Institute of EducationNanyang Technological University [email protected]
- 2. IntroductionThis seminar focuses on the key competencies required to handle challenging mathematics problems at primary school level.
- 3. Part 1This section explains the PSLE format.
- 4. PSLE MathematicsPaper 1 (50 min)Paper 2 (1 hr 40 min)
- 6. Part 2This section explains the curriculum that the PSLE is based on.
- 7. PSLE Mathematics is Based on a Problem-Solving Curriculum
- 9. rationale of the curriculumThe rationale of teaching mathematics is that it is “a good vehicle for the development and improvement of a person’s intellectual competence”.
- 10. Part 3This section explains that problem solving is a basic ability in the PSLE.
- 11. “Mathematical problem solving is central to mathematics learning.” Ministry of Education 2006
- 12. Ali paid for a 85-cent pen with a $5 note.How much change should he get?Answer: $__________Example 1
- 13. A show started at 10.55 a.m. and ended at 1.30 p.m. How long was the show in hours and minutes?Example 2
- 14. Prawns are sold at $1.35 per 100 g at a market. What is the price of 1.5 kg of prawns? $13.50 + $6.75 = $20.25Example 3
- 15. During a sale, mugs are sold in sets of 3 for $1.45. How much must Bala pay for buying 15 mugs during the sale?$1.45 x 5 = $14.50 ÷ 2 = $7.25Example 4
- 16. Sam had 295 eggs. He packed all the eggs into boxes of 9 with some left over. How many eggs are left over? 29527025295 ÷ 9 = (30 + 2) remainder 77 eggs are left overExample 5
- 17. Mr Tan rented a car for 3 days. He was charged $155 per day and 60 cents for every km that he travelled. He paid $767.40. What was the total distance that he travelled for the 3 days?$767.40 – 3 x $155 = $302.40$302.40 ÷ 60 cents per km = 504 kmExample 5
- 18. Mr Tan rented a car for 3 days. He was charged $155 per day and 60 cents for every km that he travelled. He paid $767.40. What was the total distance that he travelled for the 3 days?767.40 – 3 x 155 = 302.40302.40 ÷ 0.60 = 504 He travelled 504 km.Example 5
- 19. Find <y in the figure below.360o – 210o = 150o70 o70 oy70 oExample 6
- 20. Part 4This section explains that there are other competencies in mathematics learning e.g. practical skills.
- 21. Basic Skillscomputation and procedures is not everything
- 22. The height of the classroom door is about __.(1) 1 m(2) 2 m(3) 10 m(4) 20 mExample 7
- 23. Part 5This section explains the key competencies in solving challenging problems.
- 24. ““… including non-routine, open-ended and real-world problems.”Ministry of Education 2006
- 25. MN = ABAB = BC (ABCD is a square)BC = PQPQ = MQ = NQSo, MN = MQ = NQTriangle MNQ is equilateral.Angle MNQ is 60o.Example 8
- 26. MN = Triangle AQP is isosceles. Angle MQP is 30o.Angles QMP is (180o – 30o) ÷ 2 = 75oAngles MPN is 2 x 75o = …Example 8
- 27. Part 6The ability to monitor thinking as students read – metacognition as well as the ability to show working – communication are the other important competencies.
- 28. Mrs Hoon made some cookies to sell. 3/4 of them were chocolate cookies and the rest were almond cookies. After selling 210 almond cookies and 5/6 of the chocolate cookies, she had 1/5 of the cookies left.How many cookies did Mrs Hoon sell?almond cookies5/83/8210chocolate cookies1/53/8 – 1/5 = 7/40 210 1/40 30Example 1032/40 960She sold 960 cookies.
- 29. Example 11
- 30. Parents Up In Arms Over PSLE Mathematics Paper TODAY’S 10 OCT 2009SINGAPORE: The first thing her son did when he came out from the Primary School Leaving Examination (PSLE) maths paper on Thursday this week was to gesture as if he was "slitting his throat". "One look at his face and I thought 'oh no'. I could see that he felt he was condemned," said Mrs Karen Sng. "When he was telling me about how he couldn't answer some of the questions, he got very emotional and started crying. He said his hopes of getting (an) A* are dashed." Not for the first time, parents are up in arms over the PSLE Mathematics paper, which some have described as "unbelievably tough" this year. As recently as two years ago, the PSLE Mathematics paper had also caused a similar uproar. The reason for Thursday's tough paper, opined the seven parents whom MediaCorp spoke to, was because Primary 6 students were allowed to use calculators while solving Paper 2 for the first time. …Said Mrs Vivian Weng: "I think the setters feel it'll be faster for them to compute with a calculator. So the problems they set are much more complex; there are more values, more steps. But it's unfair because this is the first time they can do so and they do not know what to expect!" …"The introduction of the use of calculators does not have any bearing on the difficulty of paper. The use of calculators has been introduced into the primary maths curriculum so as to enhance the teaching and learning of maths by expanding the repertoire of learning activities, to achieve a better balance between the time and effort spent developing problem solving skills and computation skills. Calculators can also help to reduce computational errors." …Another common gripe: There was not enough time for them to complete the paper. A private tutor, who declined to be named, told MediaCorp she concurred with parents' opinions. "This year's paper demanded more from students. It required them to read and understand more complex questions, and go through more steps, so time constraints would have been a concern," the 28-year-old said.
- 32. chocolatessweets12Jim12181212121218Ken3 parts 12 + 12 + 12 + 12 + 18 = 661 part 22Half of the sweets Ken bought = 22 + 12 = 34So Ken bought 68 sweets.
- 33. Visualization – an intellectual competence - is one of the most important ability in solving problems
- 34. Part 7Students have been given opportunities to develop visualization in the six years in primary school.
- 35. Learning Basic Skillsemphasis on visualization in the learning process
- 37. My Pals Are Here! Mathematics 4A
- 38. Shaping Maths 2A
- 41.
- 42. Shaping Maths 4B
- 43. Catholic High School (Primary)
- 44. Part 8This section summarizes the five key competencies in mathematics.
- 45. 9 cm26 cm2With visualization, one does not need to know a formula to calculate the area of a trapezium.
- 46. Keys Grade School Manila
- 47. P S L E1 2 3 45 6 7 89 10 11 1213 14 15 16
- 48. Five Key CompetenciesVisualizationNumber SenseMetacognitionCommunicationPatterns – this was shown in the opening problem (see Beads Problem)










