![Lesson Plan in Math 6 for Demo-Teaching [Division of Integers]](https://cdn.slidesharecdn.com/ss_thumbnails/lessonplaninmathematics6divisionofintegers-190930130204-thumbnail.jpg?width=560&fit=bounds)
More Related Content
What's hot (20)
Similar to Translations of real-verbal expressions into letters or symbols and vice versa. (20)
Recently uploaded (20)
Translations of real-verbal expressions into letters or symbols and vice versa.
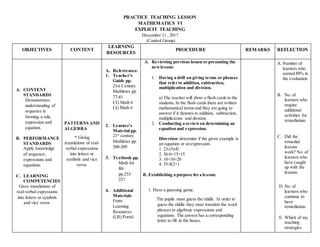
- 1. PRACTICE TEACHING LESSON MATHEMATICS VI EXPLICIT TEACHING December 11 , 2017 (Control Group) OBJECTIVES CONTENT LEARNING RESOURCES PROCEDURE REMARKS REFLECTION A. CONTENT STANDARDS Demonstrates understanding of sequence in forming a rule, expression and equation. B. PERFORMANCE STANDARDS Apply knowledge of sequence, expressions and equations. C. LEARNING COMPETENCIES Gives translations of real-verbal expressions into letters or symbols and vice versa. PATTERNS AND ALGEBRA * Giving translations of real- verbal expressions into letters or symbols and vice versa. A. Referrences: 1. Teacher’s Guide pp. 21st Century Mathletes pp. 77-81 CG Math 6 LG Math 6 2. Learner’s Material pp. 21st century Mathletes pp. 200-209 3. Textbook pp. Math for life pp.233- 237 4. Additional Materials From Learning Resources (LR) Portal A. Reviewing previous lesson or presenting the newlesson: 1. Having a drill on giving terms or phrases that refer to addition, subtraction, multiplication and division. a) The teacher will show a flash cards to the students. In the flash cards there are written mathematical terms and they are going to answer if it denotes to addition, subtraction, multiplication and division. 2. Conducting a reviewon determining an equation and expression. Direction:determine if the given example is an equation or an expression. 1. 23-(5x4) 2. 36-6=15+15 3. 10+10=20 4. 55-8(2+) B. Establishing a purpose for a lesson: 1. Have a guessing game. The pupils must guess the riddle. In order to guess the riddle they must translate the word phrases to algebraic expressions and equations. The answer has a corresponding letter to fill in the boxes. A. Number of learners who earned 80% in the evaluation. B. No. of learners who require additional activities for remediation. C. Did the remedial lessons work? No. of learners who have caught up with the lessons. D. No. of learners who continue to have remediation. E. Which of my teaching strategies
- 2. 5. Other Learning Resources Indoor and outdoor real objects, pictures, videos, laptop, TV, Charts Riddle : I am an even number. I have fluffy and I have no end. 1. thirty diminished by ten (E – 30-10) 2. twelve plus thirty six (I – 12+36) 3. Four friends share a box of pens. Each receives 3 pens. Solve to find out the equation. (G – 4x3=12) 4. The product of three and two will result to six. (H- 3x2= 6) 5. The sum of twenty and five. (T – 20+5) C. Presenting the problem opener Sam’s family bought 5 tickets for P150 each and used 3 coupons for P100 each. Write an expression to this problem? (5 x 150) – (3 x 100) Five for 150 each = 5 x 150 Used = subtract or diminished 3 coupons for P100 each = (3 x 100) worked well? Why did this work? F. What difficulties did I encounter which my principal or supervisor can help me solve? G. What innovation or localized materials did I use to discover which I wish to share with other teachers? D. Discussing newconcepts and practicing new skills 1. Translating Word Phrases into Expressions. Symbol Key Words or Phrases + Addition, plus, the sum, more than, added to, increased by, the total of - Subtraction, minus, the difference of, less than, decreased by, diminished by, subtracted from, less x, (), Multiplication, times, the product of twice, multiplied by, of
- 3. ÷, , / Division, divided by, the quotient of, the ratio of = Is equal to, equals, is, is the same as, result is , yields Translate: 1. Four increased by two Ans: 2+4 Ask: Aside from increased what other terms can we used to represent addition? b. four increased by two is equal to six. Ans. 2+4=6 Ask: Who can rephrase the word phrase? 2. The product of twenty and four 20x4 Ask: Aside from increased what other terms can we used to represent multiplication? b. The product of twenty and four is eighty 20x4=80 Ask: Who can rephrase the word phrase? Examples: 1. Six more than four times eight Ans. (4x8)+6 2. The sum of a seven and five is twelve.
- 4. Ans. 7+5=12 3. Twice the sum of 8 and two is 20. Ans. 2(8+2) = 20. 2. Independent Practice Say: Translate the following to expressions and equation. 1. five times three decreased by 25 Ans. (5x3)-25 2. the quotient of twelve and three Ans. 12÷3 3. twenty decreased by nine is equal to eleven Ans. 20-9=11 E. Finding practical applications of concepts in daily living. Form three groups. Translate this expression into word phrase. (3 +2)-4 = 1 F. Generalization How can you translate real-verbal expressions into letters or symbols? G. Evaluating Learning I. Direction: Translate the following. 1. fifty less than two 2. twenty divided by four is equal to five. 3. a one hundred decreased by fifty is fifty.
- 5. Prepared and Demonstrated by:APRIL ROSE ANIN, Student Teacher Checked by: EMILYN D. ESCAMILLA – T – III Cooperating Teacher Translate to word phrase. 4. (3x2)+4=10 5. 8 – 4 H. Additional activities for application. Translate: A number decreased by 2 is equal to twenty two. What is the number?