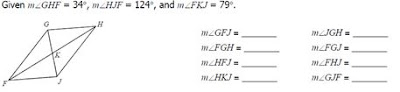Currently reading Mathematical Mindsets by Jo Boaler and continuously stewing over some geometry problems I 'taught' last year.
I need your help.
I did numerous examples with students and students did numerous examples with each other. But I don't know that I actually taught them how to problem solve. To me, these type of problems are very intuitive. How do I make students feel that way?
I didn't give students anything to figure out. I did an example for them, then asked students to do an identical example with different numbers. I didn't ask students to notice or wonder anything. I didn't ask students to think about any patterns.
This has literally bothered me for over two months now. When I would 'help' students and ask them if they had checked their notebook, more than one told me "My notebook doesn't help me." Looking at worked examples was not helpful because I didn't give them anything to make meaning out of. There was nothing to help them do the problems.
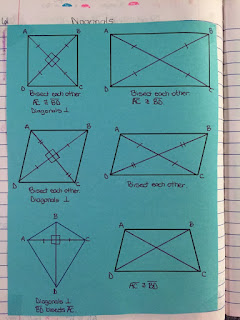
Problem Type 1: The Rectangle
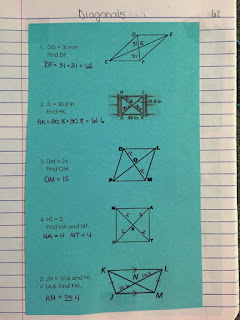
It's easy enough for students to figure out and remember that the opposite sides are equal. It's also pretty normal for them to know the diagonals are equal to each other and you can even cut them in half. Then it's pretty easy for them to agree that alternate interior angles are equal. It's a step up for them to know intuitively that each vertex is a 90 degree angle and actually be able to find the measures of the alternate interior angles. It's a bigger step up to realize this diagram contains 4 right triangles and that you need to use the Pythagorean Theorem to find the side lengths or diagonal length. And then piling more and more steps....Angle EDA is the same as angle EAD because there's also an isosceles triangle in here..Then we can use the triangle sum theorem to find angle AED.
And then there's the leap to giving them 3 values and asking them to find 8 other values while also switching back and forth between sides and angles.
Problem Type 2: The Parallelogram
The parallelogram jacks up everything. The diagonals aren't congruent anymore. The opposite vertex angles are congruent but no longer equal to 90. There's no more right triangles, Pythagorean Theorem, or isosceles triangles. But we can still find all the same values.
It just seems like so much. So many different values to find using different strategies. The two problems almost undo each other. "Hey, you know all those things you just figured out? Yeah, they no longer apply and will mess up everything if you try to use them."
How do I give students an experience or notes to look at that actually explain to them how to find these values?
All I have come up with so far is giving them a variety of diagrams with some values already given and ask them to look for patterns. Then they could write down and color code relationships. I also thought about creating a parallelogram and rectangle that they could cut apart or lift up flaps to write the relationships between them.
How do I make these problems make sense instead of like I am just pulling numbers and strategies and out of thin air? {BTW, why do we say out of thin air like air can be thin or fat? Hmm...}
How do I make this into a puzzle where students can figure out meaningful relationships between angles, sides, and missing values?


.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)