Saturdays we walk to the farmers market. It's two miles from our house. We visit our favorite booths, visit with our favorite market friends and, every summer, make new friends too. And, we go to see the kittens the animal shelter brings every week.
The kitties (and the assorted teenagers who hang out with them) are all housed inside the lobby of City Hall. Today, the two grey kittens were darling and the young woman who my almost eight-year-old has dubbed "the dramatic teenager' was teaching my kid how to sing.
I found myself with some (incredibly rare) time to think my own thoughts. My phone got boring quite quickly, but I noticed some art on the walls so I wandered over to take a look. Turns out they were prints of rubbings made from sewer covers, one of my very favorite places to find fascinating visual math.
The first picture has a fun math-y overlay in the reflection...see it?
So much to look at and take in.
I went and found a comfy bench and pulled out my notebook and a not-very-sharp pencil. From across the lobby I could see my favorite image, the one with squares in a circle. Satisfied with sitting I squinted across the space and tried to figure out how many squares made the inner circle.
And then I started doodling.
At first I tried to freehand some squares in a circle. I thought about angles. I thought about how I didn't want there to be eight, because that's too easy. So, I picked ten. I thought about what it meant to freehand a circle. I thought about how I liked that using an un-sharp pencil made me really think about precision. I thought about how I was getting better at spacing ten dots around each circle. I asked myself, how many different ways can I connect these dots to make something interesting?
On the walk home, things literally came full circle when we saw this:
I love Saturdays.
The Math in Your Feet Blog | Constructing an Understanding of Mathematics
Showing posts with label circles. Show all posts
Showing posts with label circles. Show all posts
Saturday, May 25, 2013
Sunday, April 7, 2013
Sidewalk Math: Circle Fractions, Division and Multiples
Okay, so we've walked past these two covers about a million times but today I saw them in a completely different light.
This winter/spring we've been doing a LOT with number multiples and conceptualizing multiplication and division. Last week my mind moved toward the inevitable: fractions. Although shivers go down my spine every time I think about fractions I'm still resolved to figure it all out for the sake of my seven year old, if not myself. It's been sitting in the back of my mind so I guess that's why this cover caught my eye and brought me to a dead stop.
Can you see it? Fractions and multiples!
And, a little further on, this beauty: an 8-star and some fractions!
What I really want to know is who designs these? I want that job. To see some other cool round things we found on a walk last spring, go read my post Channeling Tana Hoban: Juxtaposition Edition. Now that was one amazing day for circles!
This winter/spring we've been doing a LOT with number multiples and conceptualizing multiplication and division. Last week my mind moved toward the inevitable: fractions. Although shivers go down my spine every time I think about fractions I'm still resolved to figure it all out for the sake of my seven year old, if not myself. It's been sitting in the back of my mind so I guess that's why this cover caught my eye and brought me to a dead stop.
Can you see it? Fractions and multiples!
And, a little further on, this beauty: an 8-star and some fractions!
What I really want to know is who designs these? I want that job. To see some other cool round things we found on a walk last spring, go read my post Channeling Tana Hoban: Juxtaposition Edition. Now that was one amazing day for circles!
Saturday, January 5, 2013
Teeny Tiny Translucent Tetrahedron
material: cookie divider paper
design source: wholemovement how to fold circles
design source: wholemovement how to fold circles
sense of proportion provided by: tetrahedron made from paper plate
Friday, December 28, 2012
Circle Discoveries
I went to the Y. I came back.
"Look, Mama, I've been discovering things about circles while you were gone."
"Oh really? What did you discover?"
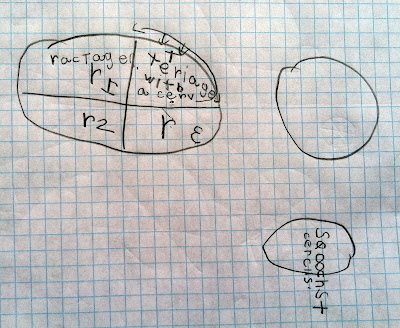
(It looks like she discovered an old pad of graph paper and was exploring a drawing of concentric circles made by me a while back - she drew in the divisions -- and then moved on to make one of her own with a compass.)
"Well, I discovered that there are lots of ways to divide a circle...and I discovered that no matter how big or small a circle is you can still divide it the same way."
"Well, that's very interesting! But what's this?"
"This is a cylinder and these are circles."
"Cool! And what's this one?"
"These are ovals. They're squooshed (sic) circles. This one has one triangle with a curve and the others are rectangles."
"Hmmm...I don't think I agree with that. Remember that a rectangle has to have four right angles. That's why they call it a rec-tANGLE..."
"Oh...yeah."
I really think that using geometry and shapes to explore number concepts is a strong combination. I've been working on a new idea that's sort of algebraic, geometric and numeric all at once. Since the kid seems to be experiencing a post-holiday renaissance I might just be able to finish up the activity with her some time soon. Stay tuned!
"Look, Mama, I've been discovering things about circles while you were gone."
"Oh really? What did you discover?"
(It looks like she discovered an old pad of graph paper and was exploring a drawing of concentric circles made by me a while back - she drew in the divisions -- and then moved on to make one of her own with a compass.)
"Well, I discovered that there are lots of ways to divide a circle...and I discovered that no matter how big or small a circle is you can still divide it the same way."
"Well, that's very interesting! But what's this?"
"This is a cylinder and these are circles."
"Cool! And what's this one?"
"These are ovals. They're squooshed (sic) circles. This one has one triangle with a curve and the others are rectangles."
"Hmmm...I don't think I agree with that. Remember that a rectangle has to have four right angles. That's why they call it a rec-tANGLE..."
"Oh...yeah."
I really think that using geometry and shapes to explore number concepts is a strong combination. I've been working on a new idea that's sort of algebraic, geometric and numeric all at once. Since the kid seems to be experiencing a post-holiday renaissance I might just be able to finish up the activity with her some time soon. Stay tuned!
Sunday, April 22, 2012
Circularity
For some reason, I had circles in my head. Last night I gathered up a bunch of different sizes of circles...
...and this morning I taught the kid how to use a compass. It took a little practice, but she got the hang of it fairly quickly.
She played around with concentric circles, circles that 'go off the page' and even discovered that three circles together can 'make a triangle!'
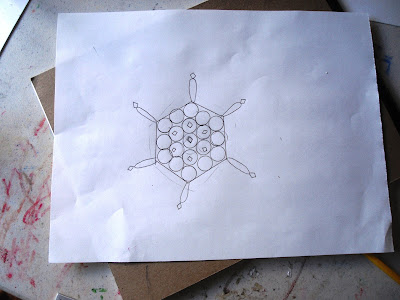
While she played around, I took a paper plate and a CD. With the CD centered inside the paper plate, I drew one circle tracing the small circle in the center of the disc. Then I played around...until, WOW! Look at that! I made a hexagon! I felt like I had just discovered a dinosaur bone or something. I decided to color it in to highlight the structure.
At that point it was time to go do Sunday things, but it took forever to get out the door. The kid kept finding circles everywhere.
When we got home from Sunday things, we started in on it again. This time, the kid started experimenting with tracing the circles. A straw can make a smaller circle than the compass can.
I made another hexagon out of circles, but colored it in differently, the kid's favorite it turns out.
The kid constructed two different versions of concentric circles (mostly using the compass). "See Mama! They're the reverse of each other. This one has a lot of rings on the inside, but not on the outside. The other circle is the opposite!"
And, then, she wanted to make a hexagon like mine so I showed her how to use the CD center circle. I really like her design sensibility. It's so different from mine.
And then it was time for lunch, but we still have unanswered questions waiting to be resolved. Like, what else can you make with the compass besides circles inside circles? Great question, kid.
I'm fairly certain we've only just begun...
Tuesday, November 30, 2010
Math & Movement Lesson: Basketball Court Pathways
Ooooh, I just had an idea! Last year I developed a preschool math/movement program by creating simple pathways through an empty space with different colored tape on the floor, and adding locomotor movements down the different paths. Within a couple months the kids could follow more complex pathways using combinations of locomotor movements.
I've been thinking recently that what I did with four year olds could be adapted for the K-2 set. The problem is that putting down tape can take a long time. However...
Most public schools and sports centers have a gym. A gym with lines already on the floor. Basketball court kinds of lines. Lines that are straight and curved. (It's hard to make curved lines with tape. Really hard.) To take advantage of all these lines and all the open space, here's an idea to use with five-to-eight year olds that I came up with that merges an exploration of space with locomotor movements.
The lesson, below, is definitely in the 'map is not the territory' category. I've had the idea, I've based it on previous experience, I've mapped it out for you to try, but we won't know how it works until someone tries it out. That's one of the reasons I am sharing this lesson, because I probably won't have a chance in the near future to try it out with kids and it seems like such an exciting idea!
The lesson is more like a whole unit of activities and you'll need to decide how to break it up into manageable chunks. Also, since repetition is the key to learning, I encourage you to repeat a lesson until it's clear that everyone understands it physically and cognitively. In even smaller chunks it could also serve as a movement break when needed in the course of a learning day.
Finally, this lesson starts out looking a lot like dance, and it will build dance skills. As you build those skills, the more math you'll be able to explore. If you try out any aspect of this lesson I'd really love to hear how it went and if you have any suggestions or questions. And, I'd love to hear from you because I'll have questions for you, too! Leave a comment here or e-mail me at: malke (dot) rosenfeld (at) earthlink (dot) net!
Basketball Court Pathways
©2010 Malke Rosenfeld, http://www.mathinyourfeet.blogspot.com/ and http://www.mathinyourfeet.com/
Users of this lesson have permission to share it with others with proper acknowledgement, copyright notice, and website links (as above). If you want to share this lesson with forums, educational groups, wiki sites, etc. please consider sending me a message to let me know where you put it. You can e-mail me at: malke (dot) rosenfeld (at) earthlink (dot) com
LESSON OVERVIEW:
After exploring a variety of paths around a basketball court by following the lines, 5 to 8 year olds will:
LEARNING GOALS:
Children will:
VOCABULARY:
Locomotor Movements: skip, hop, run, walk, slide, gallop, hop, leap, jump
Other Movements & Attributes: turn, smooth, sharp, slow, quick, big, small, long, short, high, low
Spatial/Directional Terms: left, right, on, around, curve, straight, forward, backward, corner, on, off, double, single, length (time and distance), intersecting lines
MOVEMENT ACTIVITIES:
MAPPING ACTIVITIES:
EXTENDING THE ACTIVITY:
Remember, the movement itself is furthering spatial understanding and this experience (up through the mapping, above) may be enough for five to eight year olds. However, if you think your kids are ready, here are some additional suggestions to further the exploration of math concepts:
MUSIC SUGGESTIONS:
This music is essentially for background color during the creative work. Dancing to the beat is a whole other ball of wax, so please just start out using the music as inspiration for the creative work time. That being said, you can spend some parts of your dancing time just on locomotor movements, and that would be a good time to work on dancing to/with the beat.
Artist/Album/Song -- all on iTunes
Chiwoniso/Rebel Woman/Listen to the Breeze (Modern African)
Vishten/Live/Figeac (Traditional Canadian)
Solas/Sunny Spells/paddy taylor's (Traditional Irish)
 |
| Look at all those lines! |
Most public schools and sports centers have a gym. A gym with lines already on the floor. Basketball court kinds of lines. Lines that are straight and curved. (It's hard to make curved lines with tape. Really hard.) To take advantage of all these lines and all the open space, here's an idea to use with five-to-eight year olds that I came up with that merges an exploration of space with locomotor movements.
The lesson, below, is definitely in the 'map is not the territory' category. I've had the idea, I've based it on previous experience, I've mapped it out for you to try, but we won't know how it works until someone tries it out. That's one of the reasons I am sharing this lesson, because I probably won't have a chance in the near future to try it out with kids and it seems like such an exciting idea!
The lesson is more like a whole unit of activities and you'll need to decide how to break it up into manageable chunks. Also, since repetition is the key to learning, I encourage you to repeat a lesson until it's clear that everyone understands it physically and cognitively. In even smaller chunks it could also serve as a movement break when needed in the course of a learning day.
Finally, this lesson starts out looking a lot like dance, and it will build dance skills. As you build those skills, the more math you'll be able to explore. If you try out any aspect of this lesson I'd really love to hear how it went and if you have any suggestions or questions. And, I'd love to hear from you because I'll have questions for you, too! Leave a comment here or e-mail me at: malke (dot) rosenfeld (at) earthlink (dot) net!
Basketball Court Pathways
©2010 Malke Rosenfeld, http://www.mathinyourfeet.blogspot.com/ and http://www.mathinyourfeet.com/
Users of this lesson have permission to share it with others with proper acknowledgement, copyright notice, and website links (as above). If you want to share this lesson with forums, educational groups, wiki sites, etc. please consider sending me a message to let me know where you put it. You can e-mail me at: malke (dot) rosenfeld (at) earthlink (dot) com
LESSON OVERVIEW:
After exploring a variety of paths around a basketball court by following the lines, 5 to 8 year olds will:
- decide on a pathway that has a clear beginning, middle and end;
- create a pathway that includes both straight and curved lines as well as directional interest and some repetition;
- decide on two to three locomotor movements (skip, hop, run, walk, slide, gallop, hop, leap, jump) to use while moving down the pathway and which part of the pathway gets what movement;
- map out the pathway on paper, including color coding and notating when and where to do their movements.
LEARNING GOALS:
Children will:
- Use intentional, meaningful movement to gain experience and competency with spatial relationships, a foundation for mathematics understanding;
- Make creative choices about the length, shape, direction and design of the pathway;
- Express creative choices with appropriate math and dance terminology;
- Bring their kinesthetic experience to the symbolic realm on the page by creating a simple map of their dance; and,
- When appropriate, integrate the concept of scale and coordinate systems when mapping the pathway.
VOCABULARY:
Locomotor Movements: skip, hop, run, walk, slide, gallop, hop, leap, jump
Other Movements & Attributes: turn, smooth, sharp, slow, quick, big, small, long, short, high, low
Spatial/Directional Terms: left, right, on, around, curve, straight, forward, backward, corner, on, off, double, single, length (time and distance), intersecting lines
MOVEMENT ACTIVITIES:
- Start by playing follow-the-leader around the gym to introduce kids to the different combinations of straight and curved pathway choices. Start by walking on the lines -- as long as you stay on a line you're playing the 'game' right. Model the idea of a starting and ending ___location by saying "We'll start at this corner, where should we finish our path?" and "Now we have finished this path, where should we start the next one?"
- As you play this introductory game, start giving kids choices about which locomotor movements to use (skip, hop, run, walk, slide, gallop, hop, leap, jump). You can stay in the lead or give kids turns taking the lead which will help keep the game fresh. Spend as long as you like on this, and perhaps even repeat the activity a few times a week for a couple weeks. You can vary this 'game' by giving different challenges such as: 'How slowly can we move this time?' or 'How smoothly can we move?' or 'When we turn a corner, let's make it a sharp turn!' or 'Let's make our movements big on the straight lines and small on the curved lines.' Keep it playful!
- After you're sure they have the 'follow the lines' concept, put on some music (examples below) and let the kids experiment with the lines to find their own pathways. At this point it should just be about the path, not the movements. The goal is that eventually every person should have their own unique pathway. After they've experimented for a couple minutes, have them 'freeze' and reinforce this goal as well as the...
- Rules of the Road: If they cross paths or eventually share part of a pathway with another child, challenge them to be 'good drivers' and share the road. Also, remind them that they need: a starting point and an ending point, to use at least 1/4 of the gym, and to include repetition (for example, two trips around a circle, or double back down a line).
- Let them work for two minutes then gather them in a group and see who wants to share their work. Ideally, pick a kid who looks like s/he already has a pathway and is able to repeat it. Get a couple kids to show first then send everyone back out to finalize a pathway they can repeat the same way every time.
- Make sure every kid gets to show his or her pathway before moving on. Use this time to give feedback; you'll want to make evaluative comments like "The lines you've chosen are all straight lines. I wonder what it would look like if you added a curved line to your path?" or anything else you've noticed about their work. Because this is a creative activity, there is no completely wrong answer/path, just decisions to make. So, try to pose questions that will help the child become conscious of the decisions s/he is making. When everyone has shared their work, this may be a good time to stop the lesson for the day. Or, it may be a good time to go directly to the Mapping Activities section and complete Activity #1.
- Once everyone has a pathway, take some time away from the paths to review basic locomotor movements by saying, "Who knows what a gallop looks like? Who would like to show me what a gallop looks like? That's right, one foot in front of the other!" Have one child at a time illustrate the different locomotor movements, naming each one as you go. This is essentially a mini-lesson focusing on locomotor movements where kids get a chance to practice their locomotor movement skills by follow one of the lines on the court instead of a more complicated pathway. That's a good way to assess where their skills are at. You can never do too much of this kind of cross-lateral movement, which is why this is good for a movement break as well as a dance/math lesson.
- By now, you should have decided on your own pathway too. The next step is to add locomotor movements to the pathways, so model for them what you are going to do with your path. The best bet is to have one choice of movement per line and then change to a different movement when the line changes (straight to curved, or after you turn a corner.)
- Some final reminders for the pathways: turn all corners sharply, and find smoother movements for moving on the curved lines, which will enhance the attributes of a curve.
MAPPING ACTIVITIES:
- Have kids review their pathways. Using black marker, pen or pencil, have them draw their pathway as best they can on a piece of unlined paper.
- Make a little key of the movements used while traveling the pathway. Write the moves down (i.e. skip, run, hop) and assign a color to each move.
- Redraw the pathway on a second piece of paper, this time using the assigned colors to create each section of the pathway. An alternative would be to color the existing black-lined map using the assigned colors.
- If you think it would work (7 or 8 year olds) have the kids trade maps and see if they can recreate the other person's pathway.
EXTENDING THE ACTIVITY:
Remember, the movement itself is furthering spatial understanding and this experience (up through the mapping, above) may be enough for five to eight year olds. However, if you think your kids are ready, here are some additional suggestions to further the exploration of math concepts:
- Have the kids assign a certain number of skips, hops, gallops, etc. to each section of their pathway. Make sure it can be danced first, and then transfer to the page.
- Measure the space and the length of the lines and then create a scale drawing/map of the pathway.
- Using the measurements of the space (above), create a scaled-down version of the pathway using an x and y coordinate grid. The intersection of x and y would be oriented to the center of the space your path runs through.
- Develop beat competency. Using one of the music selections below, work on moving 'to the beat' while moving on the pathway.
- Basic phrasing. Each line segment in the pathway will have a certain length which can accommodate a certain number of steps. Kids can figure out how many hops they can do on the line before getting to the corner or the start of the curve and then mark that on their map. Which brings up another point...
- How many small hops on the line? How many if you do your hops bigger? An issue of scale, I suppose. Lots of experimentation and questions (from you and the kids) along with a 'let's try it' kind of attitude can bring out some amazing math connections that none of us know are there yet! Let me know what you find out!
MUSIC SUGGESTIONS:
This music is essentially for background color during the creative work. Dancing to the beat is a whole other ball of wax, so please just start out using the music as inspiration for the creative work time. That being said, you can spend some parts of your dancing time just on locomotor movements, and that would be a good time to work on dancing to/with the beat.
Artist/Album/Song -- all on iTunes
Chiwoniso/Rebel Woman/Listen to the Breeze (Modern African)
Vishten/Live/Figeac (Traditional Canadian)
Solas/Sunny Spells/paddy taylor's (Traditional Irish)
Saturday, November 6, 2010
Picture Perfect

A few weeks ago I published a post about focusing on transitions in a moving classroom. To illustrate the post, I looked around the internet for a picture of a color wheel to show the transitions of colors changing from one into another, but wasn't satisfied with anything I found.
Moments after I published the post, this picture showed up in my inbox! It's from my dancing friend in Minnesota, Julie Young, illustrating the many colors of a northern fall. She had no idea at the time that she had just sent me the very thing I had been looking for. Actually, it was much, much better than I had been hoping for.
If a picture is worth a thousand words, I've already said too much. I think I'll let the beauty of nature, and my friend's creative nature, speak for themselves.
Wednesday, November 3, 2010
The Power of Limits 2: A Circle
Stephen Nachmanovitch, in his book Free Play: The Power of Improvisation in Life and the Arts, includes a chapter titled 'The Power of Limits.' This is the second in a series of posts inspired by this chapter, exploring how limits not only enhance creative problem solving but are actually a requirement of such a process.
Here's something I found today in the FAQ section of Wholemovement.com, a site dedicated to folding circles:
It will probably not surprise you to hear that Bradford Hansen-Smith, the creator/instigator of this movement, spent many years as a sculptor. I love what he is doing with circles. I feel nothing but pure, shameless joy at finding this beautiful example of the arts and math seamlessly integrated.
Here's something I found today in the FAQ section of Wholemovement.com, a site dedicated to folding circles:
From looking at the examples on this site of what you can do with folded and joined circles, it does seem that there are no limits to a circle.Most paper folding starts with a polygon shape. Origami uses square paper. The square is only part of a circle that has been cut into five pieces and four are discarded. This lacks economy. The circle has infinite diameters; the square has been reduced to two. Having no sides the circle has no limits.
It will probably not surprise you to hear that Bradford Hansen-Smith, the creator/instigator of this movement, spent many years as a sculptor. I love what he is doing with circles. I feel nothing but pure, shameless joy at finding this beautiful example of the arts and math seamlessly integrated.
Subscribe to:
Posts (Atom)