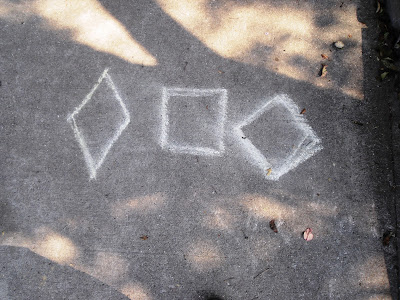The Math in Your Feet Blog | Constructing an Understanding of Mathematics
Showing posts with label geometry. Show all posts
Showing posts with label geometry. Show all posts
Thursday, August 1, 2013
Sunday, March 10, 2013
A Flood of Self-Initiated Math
So, the seven-year-old has been having a spate of self-initiated math lately. First there was her 'map of angles' and then having her dolly write an essay on 'What Infinity Means to Me'. So, I guess I wasn't too surprised to hear her from the other room giving her dolly another math lesson:
In her most patient, teacherly voice:
"I'm drawing a simple house, Amelia. Everything in the house is mostly 90 degrees...you don't have to be exactly accurate but it just has to be good...a triangle window and here's the front porch....compare these two houses. Can you fix this one? Good job!"
[Her explanation to me when I asked her later what she was doing: "I drew a house without angles and with angles and Amelia had to fix the house without angles up!"]
After Amelia's success, she continued the lesson with this explanation:
"There are even angles in nature -- straight up and down trees, but some are even 80 degrees, slanting. The old ones are 50 or 40 degrees."
Later, I got a look at her drawings:
In the larger house I see her thinking through the angles all starting from the bottom left vertex/corner of the house, which is forward movement from her original representations in the Map of Angles post. Below the big house is the 'house with angles' at the bottom and what I think is the 'house without angles' (all wonky looking) above that (I thought I saw a different drawing with the same ideas but that, apparently, has gotten lost in the shuffle.)
Another quiet moment found her exploring the structure of an isosceles triangle.
"See, there are eight of these triangles on each edge [above] and fifteen squares on the bottom edge," she told me. She also called the line she drew from the top vertex to the center of the bottom edge a "diameter" which she knows is how you divide a circle in half.
In addition to all our sidewalk math adventures over the last year, we've learned more about identifying and classifying geometric shapes in the Beast Academy 3A series but it's been a while since we did the polygons chapter. We got through skip counting which was perfect and, after entering the perimeter chapter decided to take a break. This drawing really shows me she's thinking very specifically about the length of each edge.
And, finally, although this may seem more in the 'art' category, I know for sure that drawing three-dimensionally has all kinds of math involved in it, I just don't know what kind, lol! Six or nine months ago she tried to sketch Platonic solids and really didn't do it very successfully. I think her eye has come a long way:
Her milk box:
An Asian ceramic bowl with some paper flowers in it:
Her electric pencil sharpener:
I love seeing (and hearing) the world through her eyes.
In her most patient, teacherly voice:
"I'm drawing a simple house, Amelia. Everything in the house is mostly 90 degrees...you don't have to be exactly accurate but it just has to be good...a triangle window and here's the front porch....compare these two houses. Can you fix this one? Good job!"
[Her explanation to me when I asked her later what she was doing: "I drew a house without angles and with angles and Amelia had to fix the house without angles up!"]
After Amelia's success, she continued the lesson with this explanation:
"There are even angles in nature -- straight up and down trees, but some are even 80 degrees, slanting. The old ones are 50 or 40 degrees."
Later, I got a look at her drawings:
In the larger house I see her thinking through the angles all starting from the bottom left vertex/corner of the house, which is forward movement from her original representations in the Map of Angles post. Below the big house is the 'house with angles' at the bottom and what I think is the 'house without angles' (all wonky looking) above that (I thought I saw a different drawing with the same ideas but that, apparently, has gotten lost in the shuffle.)
Another quiet moment found her exploring the structure of an isosceles triangle.
"See, there are eight of these triangles on each edge [above] and fifteen squares on the bottom edge," she told me. She also called the line she drew from the top vertex to the center of the bottom edge a "diameter" which she knows is how you divide a circle in half.
In addition to all our sidewalk math adventures over the last year, we've learned more about identifying and classifying geometric shapes in the Beast Academy 3A series but it's been a while since we did the polygons chapter. We got through skip counting which was perfect and, after entering the perimeter chapter decided to take a break. This drawing really shows me she's thinking very specifically about the length of each edge.
And, finally, although this may seem more in the 'art' category, I know for sure that drawing three-dimensionally has all kinds of math involved in it, I just don't know what kind, lol! Six or nine months ago she tried to sketch Platonic solids and really didn't do it very successfully. I think her eye has come a long way:
Her milk box:
An Asian ceramic bowl with some paper flowers in it:
Her electric pencil sharpener:
I love seeing (and hearing) the world through her eyes.
Wednesday, January 2, 2013
All-in-One? Using Shapes to Explore Number & Algebra Concepts
I'll start right out by saying that I'm pretty sure this was not the right activity at the right time for my 7.5 year old darling girl, but I did learn a lot about where her mathematical thinking is right now, which is always helpful.
In the last one and a half years my inquiry into elementary math education has kept pace with her math learning. We've discovered so much together and it's been an incredible learning process for both of us. Lately, though, it seems like the big picture concepts have clicked for me but as I try to move forward myself I end up rushing her. The following activity is a case in point, but I still think it has merit for some child, somewhere! Here's how it played out:
Back in November I bought a travel set of attribute blocks. We haven't done much with them yet, but after looking through the little activity booklet that came with it I found an activity that piqued my interest. It had to do with figuring out how many blocks of a certain shape (or combination of shapes) you would need to have to get a total number of sides. It looked vaguely algebraic to me but was presented as a mental math activity. So, I thought I'd create my own version of the activity on paper to make it a little easier to follow and to visually reinforce the differences between shapes.
This is the first worksheet I made. In the first example I labeled the triangle with a 1 (meaning one group of three sides) and she had to figure out how many more hexagons made it add up to a total of 15 sides. The second problem also had one shape already labeled, but in the final two problems I left it to her to figure out how many of both shapes. You can see little pencil marks around the shapes at the bottom where she counted the sides one by one and then made notes for herself.
She was not completely happy with this activity (and was in a bad mood, distracted by whether the word 'futzy' was an insult or not). Grumpy or not I think it really stretched her capacity in a good way, well enough for me to try again. In the second iteration I asked her to write the total number of sides under each shape which I think really helped. It was easier for her this time around. You also might notice that I rephrased the question a little.
Then the holidays interceded with math learning. Over that time, though, I did some thinking about how perhaps this kind of activity could be used to reinforce the concepts of multiples and the commutative property. For example, 4 three-sided shapes (triangles) have the same number of edges as 3 four-sided shapes (squares or rectangles). I also wanted to continue to stretch her idea of what the equal sign means; not necessarily a result, but a relationship -- various expressions of the same idea.
Here is the third activity. In it I intentionally grew the numbers from 6 to 12 to 24 to 48.
This time her strategy right out of the gates was skip counting whole groups of sides to work toward her answer instead of counting individual edges. This means to me that somehow in the last three weeks her brain has begun to 'group' with more facility. I think this because, in the same time period, she has also experienced a huge jump in her reading abilities -- from having to sound out familiar words as if they were new every time to simply looking at a word and knowing what it says. The math concept of 'grouping' and the reading concept of 'chunking' are essentially the same skill -- smaller items grouped into a larger whole. I saw that click into gear today with my daughter as she went to skip counting unbidden.
Anyhow, she moved through this last activity fairly quickly until the last two problems. After it was finally over she proclaimed, "That was hard! I hated it! Forty-eight is such a big number!!"
That proclamation was revealing to me -- at this point in the game she's got facility with multiples of 0,1, 2, 3, 4, 5, 10 and 11. The larger numbers are still a lot of work in terms of multiplication. Being able to decompose a number like 48 was just too much at this moment in time. Ultimately, I think it's a call to put on my own brakes and, instead of trying to rush us forward, really dig into the mysteries of number composition and decomposition. I know numbers are my weak point, so this will be good for me personally as well.
Epilogue: After drafting this post this afternoon and then leaving to let it sit for a while I ran across the multiplication card game called Snap it Up which I found a month or so ago while at Goodwill (read about moreof my thrifted math here!). I decided to give it a try and what do you know? It was fun for both of us! One interesting observation was that when I said 'what's x times y' she'd give me a blank look but when I said 'what are two fives...' or 'how many tens make eighty' she totally got it. I love it when the math stars align for us like this. It happens a lot, actually, but I am grateful each and every time.
In the last one and a half years my inquiry into elementary math education has kept pace with her math learning. We've discovered so much together and it's been an incredible learning process for both of us. Lately, though, it seems like the big picture concepts have clicked for me but as I try to move forward myself I end up rushing her. The following activity is a case in point, but I still think it has merit for some child, somewhere! Here's how it played out:
Back in November I bought a travel set of attribute blocks. We haven't done much with them yet, but after looking through the little activity booklet that came with it I found an activity that piqued my interest. It had to do with figuring out how many blocks of a certain shape (or combination of shapes) you would need to have to get a total number of sides. It looked vaguely algebraic to me but was presented as a mental math activity. So, I thought I'd create my own version of the activity on paper to make it a little easier to follow and to visually reinforce the differences between shapes.
This is the first worksheet I made. In the first example I labeled the triangle with a 1 (meaning one group of three sides) and she had to figure out how many more hexagons made it add up to a total of 15 sides. The second problem also had one shape already labeled, but in the final two problems I left it to her to figure out how many of both shapes. You can see little pencil marks around the shapes at the bottom where she counted the sides one by one and then made notes for herself.
She was not completely happy with this activity (and was in a bad mood, distracted by whether the word 'futzy' was an insult or not). Grumpy or not I think it really stretched her capacity in a good way, well enough for me to try again. In the second iteration I asked her to write the total number of sides under each shape which I think really helped. It was easier for her this time around. You also might notice that I rephrased the question a little.
Then the holidays interceded with math learning. Over that time, though, I did some thinking about how perhaps this kind of activity could be used to reinforce the concepts of multiples and the commutative property. For example, 4 three-sided shapes (triangles) have the same number of edges as 3 four-sided shapes (squares or rectangles). I also wanted to continue to stretch her idea of what the equal sign means; not necessarily a result, but a relationship -- various expressions of the same idea.
Here is the third activity. In it I intentionally grew the numbers from 6 to 12 to 24 to 48.
This time her strategy right out of the gates was skip counting whole groups of sides to work toward her answer instead of counting individual edges. This means to me that somehow in the last three weeks her brain has begun to 'group' with more facility. I think this because, in the same time period, she has also experienced a huge jump in her reading abilities -- from having to sound out familiar words as if they were new every time to simply looking at a word and knowing what it says. The math concept of 'grouping' and the reading concept of 'chunking' are essentially the same skill -- smaller items grouped into a larger whole. I saw that click into gear today with my daughter as she went to skip counting unbidden.
Anyhow, she moved through this last activity fairly quickly until the last two problems. After it was finally over she proclaimed, "That was hard! I hated it! Forty-eight is such a big number!!"
That proclamation was revealing to me -- at this point in the game she's got facility with multiples of 0,1, 2, 3, 4, 5, 10 and 11. The larger numbers are still a lot of work in terms of multiplication. Being able to decompose a number like 48 was just too much at this moment in time. Ultimately, I think it's a call to put on my own brakes and, instead of trying to rush us forward, really dig into the mysteries of number composition and decomposition. I know numbers are my weak point, so this will be good for me personally as well.
Epilogue: After drafting this post this afternoon and then leaving to let it sit for a while I ran across the multiplication card game called Snap it Up which I found a month or so ago while at Goodwill (read about moreof my thrifted math here!). I decided to give it a try and what do you know? It was fun for both of us! One interesting observation was that when I said 'what's x times y' she'd give me a blank look but when I said 'what are two fives...' or 'how many tens make eighty' she totally got it. I love it when the math stars align for us like this. It happens a lot, actually, but I am grateful each and every time.
Monday, October 15, 2012
Lunch Table Math Discovery (Video Conversation)
Listen as my seven year old shares her discoveries about our lunch table, one fine October afternoon:
This moment brought to you by our Paul Salomon-inspired star inquiry. I love the whole sequence because it captures the essence of hundreds of other math conversations and discoveries she and I have had together over the last year. They're small moments of inspiration, identification, conversation and observation that are being layered, pieced and added together into something incredible -- comprehension.
Fourth-agon. I love it.
This moment brought to you by our Paul Salomon-inspired star inquiry. I love the whole sequence because it captures the essence of hundreds of other math conversations and discoveries she and I have had together over the last year. They're small moments of inspiration, identification, conversation and observation that are being layered, pieced and added together into something incredible -- comprehension.
Fourth-agon. I love it.
Monday, September 17, 2012
A Seven Year Old's "Math Thought"
Kid, scrambling for some paper and a pencil: "Mama! Hold on a second, I have a math thought!"
Silly me, I just thought she was trying to avoid having her hair brushed... It took her three tries, but on the third try she had it just right.
Me: "Tell me about it..."
Kid: "This is a square, and if you draw two triangles you get a rhombus."
"Scrar" = square
"Robis" = rhombus
"T" = triangle
Me: "That's really cool! How did you come up with that?"
Turns out it was this funny little geometric-solid-ish toy I bought her for $6 at the local children's science museum. This is what she saw:
Silly me, I just thought she was trying to avoid having her hair brushed... It took her three tries, but on the third try she had it just right.
Me: "Tell me about it..."
Kid: "This is a square, and if you draw two triangles you get a rhombus."
"Scrar" = square
"Robis" = rhombus
"T" = triangle
Me: "That's really cool! How did you come up with that?"
Turns out it was this funny little geometric-solid-ish toy I bought her for $6 at the local children's science museum. This is what she saw:
Thursday, August 16, 2012
Starting Stars: Hexagon/Dodecagon Edition
I was recently inspired by Paul Salomon's thinking about stars and mathematics. From our conversations I am excited about trying to understand stars better myself, and also about what they might have to offer in terms of elementary math explorations with my seven year old daughter.
Paul mentioned to me that stars have connections not only to geometry, but also to number theory and group theory (a branch of modern abstract algebra). The visual interest provided by different kinds of stars is really what pulled me and my daughter in, with both of us wondering aloud: What's going on there?
I started my inquiry last night by constructing a bunch of different 12 stars. Sure I could have gone straight to the cool star applet Paul recommended, but I somehow found myself drawn to the classic geometer tools: pencil, straightedge and compass. I wasn't sure how far I'd get, but I wanted to at least understand how a dodecagon (twelve sided polygon) was constructed so my kid and I could make one using floor tape in the morning.
I used an illustration from the book Quadrivium: The Four Classical Liberal Arts of Number, Geometry, Music and Cosmology as a reference. I started with a circle 2" in diameter and then made six more circles with their centers evenly spaced around the circumference of the first circle. From there it was pretty easy to connect the dots to make a hexagon, and use the outer circles to create the points/vertices of the dodecagon....
...and that's as far as the book illustration got me.
Then, looking at a photo of twelve pointed stars Paul had designed and cut out of plexiglass (I ordered my own set, it's coming soon!) I tried drafting my own versions. Using the basic framework for the dodecagon I made two stars -- one made of two hexagons, the other out of three squares. It looks pretty straight forward, but at one point I really struggled with how to create the points of both stars -- you can see erroneous red lines in both pictures.
And here are two more stars, below; one made from four triangles, and another from a six line asterisk. There was one more that I couldn't figure out, but I was still pretty satisfied with my efforts. My lingering confusion is the system and language Paul uses to classify stars; his notation looks vaguely like Cartesian coordinates. I've read over his explanations to me, but I really wish he were across a table from me illustrating it in real life. What I notice in the picture above, for example, is that the green side of a square intersects with two points, one on either side of the red and orange points. I see it but I don't know how to talk about it yet.
I did all that last night. This morning I really wanted to see if we could at least tape down a hexagon on the floor. Despite the fact that many of my posts seem like my kid and I are in some sort of harmonious learning nirvana, she is actually sometimes quite a resistant learner which was the case today -- she really wanted nothing to do with me and my math.
However, I went ahead and started measuring out 12" edges for the floor hexagon. I had one already measured and cut but had to leave the room for some reason, and when I came back I found her doing this:
She was measuring, taping and cutting as she went and was doing an excellent job at eyeing the angles. Her fourth angle was a little too big, so I pulled in a hexagon from our pattern block set to show her how to use it to make each interior angle the same. Resistance flared again, but I had the immutable laws of geometry on my side. "Well," said I, "it won't really be a hexagon unless all the inside angles are the same." Silence.
I sat quietly by after that and at some point I noticed she had taken the yardstick to make sure all the sides were the same length. I heard her mutter something about "...these two are thirteen inches..." and then I saw she had decided to trim them. Her hexagon is below -- pretty good! Then she made sure to let me know she was making a square around it so no one would touch it. It was hers, not the math mommy's. She even went so far to install a burglar alarm in the form of percussion instruments so she would know if someone crossed over the line.
Given the mood around here today, I'm pretty happy with what got accomplished. She did a bunch of independently initiated measuring (length and angles), and applied her understanding of equal sides in an analysis of the hexagon she created. And all of that pretty much without me. Later, when we were out and about, she applied the activity to other areas of her life. One moment found her running up the zig-zaggy library ramp to the exit and exclaiming: "All you have to do is move your feet at an angle and you can run really fast up the ramp!" In a restroom she saw that the sink's drain were made of small circular holes that formed a hexagon, and congratulated herself that she wasn't calling it an octagon anymore.
I think I'll let it sit for a while, maybe long enough to order some more floor tape in a huge amount of colors. Perhaps a pile of new tape and some scissors left lying around will be enough to inspire a more collegial attitude around here!
Paul mentioned to me that stars have connections not only to geometry, but also to number theory and group theory (a branch of modern abstract algebra). The visual interest provided by different kinds of stars is really what pulled me and my daughter in, with both of us wondering aloud: What's going on there?
I started my inquiry last night by constructing a bunch of different 12 stars. Sure I could have gone straight to the cool star applet Paul recommended, but I somehow found myself drawn to the classic geometer tools: pencil, straightedge and compass. I wasn't sure how far I'd get, but I wanted to at least understand how a dodecagon (twelve sided polygon) was constructed so my kid and I could make one using floor tape in the morning.
I used an illustration from the book Quadrivium: The Four Classical Liberal Arts of Number, Geometry, Music and Cosmology as a reference. I started with a circle 2" in diameter and then made six more circles with their centers evenly spaced around the circumference of the first circle. From there it was pretty easy to connect the dots to make a hexagon, and use the outer circles to create the points/vertices of the dodecagon....
...and that's as far as the book illustration got me.
Then, looking at a photo of twelve pointed stars Paul had designed and cut out of plexiglass (I ordered my own set, it's coming soon!) I tried drafting my own versions. Using the basic framework for the dodecagon I made two stars -- one made of two hexagons, the other out of three squares. It looks pretty straight forward, but at one point I really struggled with how to create the points of both stars -- you can see erroneous red lines in both pictures.
And here are two more stars, below; one made from four triangles, and another from a six line asterisk. There was one more that I couldn't figure out, but I was still pretty satisfied with my efforts. My lingering confusion is the system and language Paul uses to classify stars; his notation looks vaguely like Cartesian coordinates. I've read over his explanations to me, but I really wish he were across a table from me illustrating it in real life. What I notice in the picture above, for example, is that the green side of a square intersects with two points, one on either side of the red and orange points. I see it but I don't know how to talk about it yet.
I did all that last night. This morning I really wanted to see if we could at least tape down a hexagon on the floor. Despite the fact that many of my posts seem like my kid and I are in some sort of harmonious learning nirvana, she is actually sometimes quite a resistant learner which was the case today -- she really wanted nothing to do with me and my math.
However, I went ahead and started measuring out 12" edges for the floor hexagon. I had one already measured and cut but had to leave the room for some reason, and when I came back I found her doing this:
She was measuring, taping and cutting as she went and was doing an excellent job at eyeing the angles. Her fourth angle was a little too big, so I pulled in a hexagon from our pattern block set to show her how to use it to make each interior angle the same. Resistance flared again, but I had the immutable laws of geometry on my side. "Well," said I, "it won't really be a hexagon unless all the inside angles are the same." Silence.
I sat quietly by after that and at some point I noticed she had taken the yardstick to make sure all the sides were the same length. I heard her mutter something about "...these two are thirteen inches..." and then I saw she had decided to trim them. Her hexagon is below -- pretty good! Then she made sure to let me know she was making a square around it so no one would touch it. It was hers, not the math mommy's. She even went so far to install a burglar alarm in the form of percussion instruments so she would know if someone crossed over the line.
Given the mood around here today, I'm pretty happy with what got accomplished. She did a bunch of independently initiated measuring (length and angles), and applied her understanding of equal sides in an analysis of the hexagon she created. And all of that pretty much without me. Later, when we were out and about, she applied the activity to other areas of her life. One moment found her running up the zig-zaggy library ramp to the exit and exclaiming: "All you have to do is move your feet at an angle and you can run really fast up the ramp!" In a restroom she saw that the sink's drain were made of small circular holes that formed a hexagon, and congratulated herself that she wasn't calling it an octagon anymore.
I think I'll let it sit for a while, maybe long enough to order some more floor tape in a huge amount of colors. Perhaps a pile of new tape and some scissors left lying around will be enough to inspire a more collegial attitude around here!
Thursday, June 14, 2012
Think Like a Straight Line
It's been a loooong time since the kid has ridden her bike. So long it seemed like the first time again today.
She felt wobbly. Steering was a challenge. So, she gave herself a pep talk as she worked to reacquaint herself with the activity.
"Okay, all I have to do is think like a straight line in geometry..."
She rode back and forth across the basketball courts chanting her new her mantra.
"Think like a straight line, think like a straight line, think like a straight line in geometry."
When she'd get to the end of the court, she'd get off the bike and turn it around. Then she figured she could make the turn without getting off.
"All I have to do when I get to the end is think like a circle...."
I'm sure she'll be back in the swing of things in no time. Plus, I love the thought that pathways have specific intentions. She's in the math, man. Totally in it.
She felt wobbly. Steering was a challenge. So, she gave herself a pep talk as she worked to reacquaint herself with the activity.
"Okay, all I have to do is think like a straight line in geometry..."
She rode back and forth across the basketball courts chanting her new her mantra.
"Think like a straight line, think like a straight line, think like a straight line in geometry."
When she'd get to the end of the court, she'd get off the bike and turn it around. Then she figured she could make the turn without getting off.
"All I have to do when I get to the end is think like a circle...."
I'm sure she'll be back in the swing of things in no time. Plus, I love the thought that pathways have specific intentions. She's in the math, man. Totally in it.
Sunday, June 3, 2012
Not 'Just Shapes'
So....we've been doing Sidewalk Math on and off since, hmmm, February? Three months or so. It's been me, mostly, getting all excited about what we're finding when we walk around town, taking pictures, oooh-ing and ahhh-ing. I have been having me some serious fun, let me tell you.
The kid (now a freshly minted seven) on the other hand... She's been there with me, she's been interested, participatory, but now? Now, when we go out, I am not allowed to pull out my camera. Ever. I am not allowed to initiate any math conversation whatsoever. Sounds horrid, except for the fact that now it's the kid who is finding math everywhere.
She ooohs over every single triangle she sees -- a scrap of fabric, a crack in the sidewalk, something on a wall. In negative space, she sees a triangle of ceiling made by a partially closed door. She even made me this triangle love note. Even the message inside is written to take the form of a triangle.
"Look Mama! When I folded the square [paper] I got two triangles. Look! Look inside!"
"Looks like four triangles to me," I replied. I've never seen someone so excited over four triangles.
She ahhhhs over concentric circles. She finds them everywhere -- even inside her cucumbers (where she also sees little stars, which, I manage to add over the adulation, are constructed with nature's numbers, Fibonacci, right? Three, five, eight...the cucumber star is three....) Seriously, this child has her eyes wide open. We're in a rest room. The baby changing fold out thing on the wall has circles, with circles inside them! Concentric circles on the sidewalk. At the bottom of the public pool. Everywhere.
And let's not forget spirals. I was making an extra effort a month ago to look for them and wasn't too successful, to tell the truth. Also, the kid kept getting them mixed up with concentric circles. It took a week or two of clarifying, on and off, to help her see the difference and... SNAP! The light went on and now she sees them everywhere -- in fences, on light posts, on clothing, all around the house. She draws them. She finds small ones, big ones, mostly man made but also a vine here and there, or when we look really closely at how a plant is growing. It's crazy. Spirals are everywhere.
Oh, and composite shapes -- rectangles made out of squares, squares made out of triangles, squares made out of squares, trapezoids made out of squares and triangles. And curves! Let's not forget them. And parallel lines! Right angles! The plaid fabric is a grid! You get the picture, right? I'm exhausted!
In the back of my head I am always observing my own mind-noise that says, "What's the big deal? They're just shapes. Kids learn about shapes in preschool." But my answer always circles (spirals?) back to the fact that the longer we keep our eyes open for it, the more familiar she has become with the possible variations and anomalies (size, rotation, tilings, etc.) that can occur in 'basic' shapes.
(An aside: It's been hard to verbally explain the difference between a rhombus and a square rotated from its traditional position, but sidewalk chalk saved the day!)
The kid (now a freshly minted seven) on the other hand... She's been there with me, she's been interested, participatory, but now? Now, when we go out, I am not allowed to pull out my camera. Ever. I am not allowed to initiate any math conversation whatsoever. Sounds horrid, except for the fact that now it's the kid who is finding math everywhere.
She ooohs over every single triangle she sees -- a scrap of fabric, a crack in the sidewalk, something on a wall. In negative space, she sees a triangle of ceiling made by a partially closed door. She even made me this triangle love note. Even the message inside is written to take the form of a triangle.
"Look Mama! When I folded the square [paper] I got two triangles. Look! Look inside!"
"Looks like four triangles to me," I replied. I've never seen someone so excited over four triangles.
She ahhhhs over concentric circles. She finds them everywhere -- even inside her cucumbers (where she also sees little stars, which, I manage to add over the adulation, are constructed with nature's numbers, Fibonacci, right? Three, five, eight...the cucumber star is three....) Seriously, this child has her eyes wide open. We're in a rest room. The baby changing fold out thing on the wall has circles, with circles inside them! Concentric circles on the sidewalk. At the bottom of the public pool. Everywhere.
And let's not forget spirals. I was making an extra effort a month ago to look for them and wasn't too successful, to tell the truth. Also, the kid kept getting them mixed up with concentric circles. It took a week or two of clarifying, on and off, to help her see the difference and... SNAP! The light went on and now she sees them everywhere -- in fences, on light posts, on clothing, all around the house. She draws them. She finds small ones, big ones, mostly man made but also a vine here and there, or when we look really closely at how a plant is growing. It's crazy. Spirals are everywhere.
Today she said, "I'm going to make a book of all these shapes. I'm going to take pictures with my camera and Papa will print them out for me." She wanted me to have nothing to do with it. Sniff. But, still. Isn't it cool that this whole thing has become completely, totally hers?!
In the back of my head I am always observing my own mind-noise that says, "What's the big deal? They're just shapes. Kids learn about shapes in preschool." But my answer always circles (spirals?) back to the fact that the longer we keep our eyes open for it, the more familiar she has become with the possible variations and anomalies (size, rotation, tilings, etc.) that can occur in 'basic' shapes.
(An aside: It's been hard to verbally explain the difference between a rhombus and a square rotated from its traditional position, but sidewalk chalk saved the day!)
Despite the doubts, my sense is that all the conversations we've been having over the last few months will eventually make geometry on the page that much more meaningful, and maybe even easy. (I can also imagine that this kind of activity also serves the larger goal of pattern recognition in any area of math she attempts.) It will all make sense because she will have seen those shapes in their natural habitats, and by identifying them and talking about them she will have made each shape hers and hers alone. And, as the structure of the universe continues to emerge in front of her very own (and open) eyes, how much more fun will her world be to play in, explore, put together, and then take apart again? A living math book, our world. Not 'just shapes', y'all. No indeed.
Check back with us in three or four years, maybe seven, and we'll see if I had it right. Something deep inside me, though, says that the more we actively do and see and investigate the structures and forms math takes (like the curvy wall constructed with straight bricks? Or, the sidewalk lines that look vaguely algebraic?) the more we can actually know math when we meet it in a more formal setting.
What I do know for sure right now is that the kid already considers herself 'good at math' and has added mathematician to her future career choices along with actress, singer, dancer, geologist, archaeologist, astronomer, writer, illustrator and cartographer.
What I do know for sure right now is that the kid already considers herself 'good at math' and has added mathematician to her future career choices along with actress, singer, dancer, geologist, archaeologist, astronomer, writer, illustrator and cartographer.
Have fun everyone! If you haven't heard yet, math is everywhere!
Monday, May 21, 2012
Play Power
Although I know it already, it never ceases to surprise me just how true it is.
Learners of all ages need the opportunity to experiment with a new medium before putting it to its more formal or expected use. Often this kind of activity is called 'playing around' which I often perceive as a derogatory term in relation to learning. But, in my experience, if you observe children at play long enough and really pay attention you will be astounded by the myriad of ways they are representing their knowledge, understanding and mastery of a subject. Play and exploration are not wasted time. In fact, I think it is exactly the kind of activity that builds the foundation of real understanding.
Here is a case in point from a recent Math in Your Feet Family Night. Having finally found success using straws and pipe cleaners as a math toy and building material with my own first grader, I decided to include it in the Family Night for the first time. I made some models of polygons and polyhedra, gave the station volunteer a quick orientation, and left the materials to be discovered.
Immediately, it was the most popular station of the eight offered that night. As the children descended, the adults followed, providing lots of helpful advice and some modeling...
...which the kids politely and assiduously ignored as they confidently forged ahead.
This initial inclination to explore the materials on their own terms was fortified by the fact that this was not officially 'school time'. There was no pressure to do things 'right', or follow the rules, or learn and use proper technique.
As a result, most kids cheerfully ignored the formula for folding a pipe cleaner in half and making a nice right angle before inserting it as a connector between two straws, and instead found their own twisty or unequal ways to make it work.
Most also ignored the nice models I had made and created their own. I had never heard of a hexagon cube, for example, but there it was!
They were having a grand time 'playing around' when I noticed something amazing happening. After a very focused exploration period, they started discovering the rules on their own!
This little one, two years old according to her brother who sat beside her, had been methodically putting pipe cleaners into the straws, one after another. It looked like a little gallery of Q-tips, someone joked.
Voila! A hexagon. No one, I suspect, expected much out of a girl so young. And yet, there she was discovering the materials and watching others around her, ultimately creating something for herself. I'd wager that if someone had insisted on sitting her down and showing her how to make a hexagon, she might have been less interested, engaged, focused and, ultimately, successful.
Children much older also experienced this same progression. Check out what her brother was building, below.
Kids kept coming up to me wanting to know if they could have the dodecahedron I made as model for the night. Sort of like a door prize? I said, "Well, no, that one's mine. But you could make your own!"
Only one girl decided to make one for herself; she also really wanted me to sit next to her while she figured it out. I provided moral support for about five minutes, and then had to 'go do something...' A few minutes later, she came and found me with a question and, still later, enlisted support from another adult so she could finally finish it. But you know what? She did all the work, she just needed help 'seeing' the structure and pattern. If we had had more time she and I could have talked how to make all the angles congruent so it would be more regular but, still...what a prize!
And that's just the math stuff and just what I noticed while watching them build. I'm sure there's more.
Learners of all ages need the opportunity to experiment with a new medium before putting it to its more formal or expected use. Often this kind of activity is called 'playing around' which I often perceive as a derogatory term in relation to learning. But, in my experience, if you observe children at play long enough and really pay attention you will be astounded by the myriad of ways they are representing their knowledge, understanding and mastery of a subject. Play and exploration are not wasted time. In fact, I think it is exactly the kind of activity that builds the foundation of real understanding.
Here is a case in point from a recent Math in Your Feet Family Night. Having finally found success using straws and pipe cleaners as a math toy and building material with my own first grader, I decided to include it in the Family Night for the first time. I made some models of polygons and polyhedra, gave the station volunteer a quick orientation, and left the materials to be discovered.
Immediately, it was the most popular station of the eight offered that night. As the children descended, the adults followed, providing lots of helpful advice and some modeling...
...which the kids politely and assiduously ignored as they confidently forged ahead.
This initial inclination to explore the materials on their own terms was fortified by the fact that this was not officially 'school time'. There was no pressure to do things 'right', or follow the rules, or learn and use proper technique.
As a result, most kids cheerfully ignored the formula for folding a pipe cleaner in half and making a nice right angle before inserting it as a connector between two straws, and instead found their own twisty or unequal ways to make it work.
Most also ignored the nice models I had made and created their own. I had never heard of a hexagon cube, for example, but there it was!
They were having a grand time 'playing around' when I noticed something amazing happening. After a very focused exploration period, they started discovering the rules on their own!
This little one, two years old according to her brother who sat beside her, had been methodically putting pipe cleaners into the straws, one after another. It looked like a little gallery of Q-tips, someone joked.
She was working on her own. She must have been at it for thirty minutes and then...she started connecting straws together!
Voila! A hexagon. No one, I suspect, expected much out of a girl so young. And yet, there she was discovering the materials and watching others around her, ultimately creating something for herself. I'd wager that if someone had insisted on sitting her down and showing her how to make a hexagon, she might have been less interested, engaged, focused and, ultimately, successful.
Children much older also experienced this same progression. Check out what her brother was building, below.
Kids kept coming up to me wanting to know if they could have the dodecahedron I made as model for the night. Sort of like a door prize? I said, "Well, no, that one's mine. But you could make your own!"
Only one girl decided to make one for herself; she also really wanted me to sit next to her while she figured it out. I provided moral support for about five minutes, and then had to 'go do something...' A few minutes later, she came and found me with a question and, still later, enlisted support from another adult so she could finally finish it. But you know what? She did all the work, she just needed help 'seeing' the structure and pattern. If we had had more time she and I could have talked how to make all the angles congruent so it would be more regular but, still...what a prize!
So, what kind of learning was happening during all this 'playing'?
I heard a teacher mention that this activity reinforced the learning they were doing in class about corners and sides. Yes, and so much more.
The side of the shape becomes a shared edge. You only need one straw for each edge. The more you build on to your initial shape, the more this aspect of intersection and sharing is apparent.
A vertex can be created from the intersection of two, three, sometimes even five different lines/edges.
Depending on what polygon or polyhedron you're making, the pipe cleaners need to be bent at different angles. An equilateral triangle's angles are different from a square's which are different yet again when you create a hexagon, or a pentagon. These are properties you might not truly understand unless you had to make them yourself. And, when every angle in a shape has to be the same, and you're the one who has to make them that way, you truly build a new understanding of 'sameness'.
And that's just the math stuff and just what I noticed while watching them build. I'm sure there's more.
All in all, a good evening's work. I think my new definition of success is when my project idea is just the starting point and, over the course of the 'lesson' not only do multiple right answers emerge but the children are satisfied with their efforts. If the resulting mess is any indication, I'd say it was an entirely satisfying evening.
Wednesday, May 16, 2012
Our New Math Studio
We've had a bunch of visitors in the last few days. We show them around our house. They see the ten million stuffed kitties. The see the kid's collection of old books, including the 120 year old speller and the 80 year old (very cool) atlas. They see the fantastic, never-ending headstand (hint: not mine). And then they walk into our sun room. "What is that?" they ask.
Why, it's our new math studio, of course! Here is the inside view for those lucky few who can fit in the door:
Here is the new math studio in use:

We have what we call our 'making studio' in another part of our house, and we make a lot of math these days, so it makes sense the kid would think of our new installation as a math studio.
How did we make this wonderful structure, you ask? Lots of newspaper, tape and pipe cleaners. You can read all the details here.
Why, it's our new math studio, of course! Here is the inside view for those lucky few who can fit in the door:
This is what you'd look like from the outside if you were sitting inside it.
Here is the new math studio in use:
And, here is an example of something that might be made inside. In this case, start with a cube and, um...square it? Cube it? Make a cube out of cubes? (We're both still learning about this math stuff.)
"I want the inside to be a different color, Mama, so you can see where the middle is."

We have what we call our 'making studio' in another part of our house, and we make a lot of math these days, so it makes sense the kid would think of our new installation as a math studio.
How did we make this wonderful structure, you ask? Lots of newspaper, tape and pipe cleaners. You can read all the details here.
Wednesday, May 9, 2012
Small Moments of Geometry
Sometimes, all you have to do is ask the question.
I was looking for more geometry to do with the kid, so I headed over to the Living Math Forum for some inspiration. Needless to say, I got great suggestions which jump started my thinking process in a big way. Not all of the suggestions worked for us at this particular moment; my daughter is not all that enamoured with computer games, for instance, even though there are a ton of great online math game resources. I also got some recommendations for building sets, but historically she hasn't been drawn to that kind of thing. Also, most of them are pretty pricey and I'm just not sure I'd want to risk the money at this point.
 One of the best suggestions for my particular learner was the book String, Straight Edge, & Shadow: The Story of Geometry by Julia E. Diggins. We found a copy at the library and are taking it a couple of pages at a time. It's a wonderful story but a bit dense, in the best possible way. There's a lot to ponder and it's worth taking a few days to process things between readings. Every time we read it we immediately find connections in our daily life.
One of the best suggestions for my particular learner was the book String, Straight Edge, & Shadow: The Story of Geometry by Julia E. Diggins. We found a copy at the library and are taking it a couple of pages at a time. It's a wonderful story but a bit dense, in the best possible way. There's a lot to ponder and it's worth taking a few days to process things between readings. Every time we read it we immediately find connections in our daily life.
My favorite thing about the book so far is the writing which weaves in and out of descriptive suppositions about how early humans discovered the circle or the right angle interspersed with conversational observations about how a child might also observe those same ideas in his or her daily activity and environment. After reading about right angles today in a chapter about early earth measurers, a simple folded piece of paper has now become our 'right angle checker.' We use it to observe how this helpful angle maintains order within our physical world allowing us to move easily through life without worry of wonky walls or telephone poles. I never knew a right angle was so interesting, useful or ubiquitous!
Anyhow, it seems geometry is everywhere, just waiting for us to find it. Such is the nature of small math moments.
For instance, the kid has really taken to what I'm calling her 'geometer training'. She's a whiz with the compass. We had an initial, and very successful, exploration of circles one Sunday and, a few days later our second round found me exploring concentric, intersecting circles. The kid tried making her own.
The picture below is when we finally decided to throw out the rules and see how many different sized squares and rectangles we could make out of the entire inventory of game pieces. For some reason, this was a lot more fun for her. I modeled counting the squares around the perimeter to determine whether it's a square or a rectangle and figuring area from multiplying length and width. I think that an adult modeling his or her thinking and problem solving process in a real-life context is one of the most potent teaching tools at one's disposal.

Sunday morning walks have become our routine and look at this beauty we found last weekend! This morning she suffered through half of a fun (to me!) book on polygons. The first half was about triangles, so next time we go out we'll be able to use our new words -- scalene, isosceles, equilateral, right angle, obtuse angle and acute angle.
I'm in the middle of prepping for a Math in Your Feet Family Night for next week. The kid really wants to go, but it's far away and she has a ridiculously early bedtime. But, I said, I could bring up a few activities from the basement. What would she like to do?
Turns out, the rotational paper pizza designs were quite engrossing.

A really tall tower of cubes, that is. My previous experience showed me that six inch straws do not hold up well under scrutiny from children, but three inch straws actually create a comparatively stable structure.
I was looking for more geometry to do with the kid, so I headed over to the Living Math Forum for some inspiration. Needless to say, I got great suggestions which jump started my thinking process in a big way. Not all of the suggestions worked for us at this particular moment; my daughter is not all that enamoured with computer games, for instance, even though there are a ton of great online math game resources. I also got some recommendations for building sets, but historically she hasn't been drawn to that kind of thing. Also, most of them are pretty pricey and I'm just not sure I'd want to risk the money at this point.
My favorite thing about the book so far is the writing which weaves in and out of descriptive suppositions about how early humans discovered the circle or the right angle interspersed with conversational observations about how a child might also observe those same ideas in his or her daily activity and environment. After reading about right angles today in a chapter about early earth measurers, a simple folded piece of paper has now become our 'right angle checker.' We use it to observe how this helpful angle maintains order within our physical world allowing us to move easily through life without worry of wonky walls or telephone poles. I never knew a right angle was so interesting, useful or ubiquitous!
Anyhow, it seems geometry is everywhere, just waiting for us to find it. Such is the nature of small math moments.
For instance, the kid has really taken to what I'm calling her 'geometer training'. She's a whiz with the compass. We had an initial, and very successful, exploration of circles one Sunday and, a few days later our second round found me exploring concentric, intersecting circles. The kid tried making her own.
In our first round of exploring circles, the kid saw a triangle when she placed three circles in this position. This time, as we sat working together, I took a minute to illustrate for her how I saw those triangles (below) -- by connecting the center points, and also by extending straight lines on the outside.
After pondering what else besides a compass might energize our study of geometry, I decided it was time to go out and purchase the game Blokus. The kid was thrilled when she found that over half of the pieces are actually mini, multi-colored pentominoes. (I also found a great pentomino puzzle generator for up to six pieces here.) The rules are not hard (all pieces of a certain color need to be touching corners to play) but the kid keeps noticing the open spaces and wanting to fill them in with the shapes instead of playing the 'touch corners' rule.
The picture below is when we finally decided to throw out the rules and see how many different sized squares and rectangles we could make out of the entire inventory of game pieces. For some reason, this was a lot more fun for her. I modeled counting the squares around the perimeter to determine whether it's a square or a rectangle and figuring area from multiplying length and width. I think that an adult modeling his or her thinking and problem solving process in a real-life context is one of the most potent teaching tools at one's disposal.
Speaking of modeling, the best way to get my kid interested in something is to be doing something interesting myself (like coloring in triangular grids) and having some 'extra' on hand for her to do as well. Sneaky Math Mama!
(My grid designs are on the left, hers on the right. I had my mind focused on rotation symmetry, but just let the kid explore as she would. Her second design, on the right side of her page shows some reflection in her design -- a bit hard to see in this picture.)
I always love finding something lovely after quiet time...

Sunday morning walks have become our routine and look at this beauty we found last weekend! This morning she suffered through half of a fun (to me!) book on polygons. The first half was about triangles, so next time we go out we'll be able to use our new words -- scalene, isosceles, equilateral, right angle, obtuse angle and acute angle.
Or, how about this? I love the stair step rectangular blocks. The girl noticed the circle first, but there is also a little square in the middle of it, and look! Small triangular blocks creating a square around the circle. Awesome!
And neither of us could resist the big red circular table with cool circular cutout decorations in the middle. It may be hard to see but the inner circle is made of little squares rotated 45 degrees and the outside ring I can't quite describe but is so lovely.
I'm in the middle of prepping for a Math in Your Feet Family Night for next week. The kid really wants to go, but it's far away and she has a ridiculously early bedtime. But, I said, I could bring up a few activities from the basement. What would she like to do?
Turns out, the rotational paper pizza designs were quite engrossing.
We talked about how each pizza slice had to have the same toppings in the same positions on each piece, a point to which she paid special attention. And, after that, it was time to put them into position so could see the overall rotation design (which might also have some reflection in it too!)
And, it's been months and months since I was obsessed with making the Platonic solids out of straws and pipe cleaners, a process she basically only observed. But, when she found out they were part of the family night she suddenly got interested in making one all by herself!

A really tall tower of cubes, that is. My previous experience showed me that six inch straws do not hold up well under scrutiny from children, but three inch straws actually create a comparatively stable structure.
Maybe I should go for a building set after all. Seems like she might be ready for it!
Subscribe to:
Posts (Atom)